Для начала напомним следующее определение:
Доверительный интервал -- интервал $(Q^*-\delta ,Q^*+\delta )$, который покрывает неизвестную величину $Q$ c надежностью $\gamma $.
Пусть нам дано исправленное среднее квадратическое отклонение $S$. Оценим неизвестное генеральное среднее квадратическое отклонение, то есть найдем доверительный интервал, который покрывает величину $\sigma $.
Для этого нам необходимо, чтобы выполнялось равенство
неравенствоОтметим, что так как среднее квадратическое отклонение больше нуля, то при $q>1$ доверительный интервал будет иметь вид:
Величина $q$ имеет табличные значения:
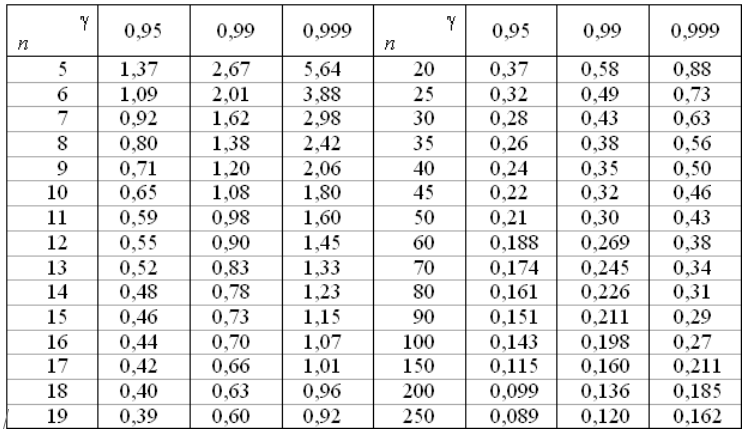
Рисунок 1. Таблица значений величины $q$.
Доверительный интеграл для оценки дисперсии
С понятием среднего квадратического отклонения тесно связано понятие дисперсии.
Пусть нам дано исправленная дисперсия. Оценим неизвестное генеральную дисперсию, то есть найдем доверительный интервал, который покрывает величину $D$.
Так как среднее квадратическое отклонение равно квадратному корню от дисперсии, то исправленная дисперсия равна квадрату исправленного среднего квадратического отклонения $S^2.$
Таким образом, получим, что доверительный интервал имеет вид:
Отметим, что так как среднее квадратическое отклонение больше нуля, то при $q>1$ доверительный интервал будет иметь вид:
Пример задач на нахождение доверительного интервала
Пусть выборка имеет исправленное среднее квадратическое отклонение $S=0,4$. Пусть объем выборки $n=60$, а надежности равна $\gamma =0,95$. Найти доверительный интервал для оценки среднего квадратического отклонения данного распределения.
Решение:
Для начала найдем величину $q$ из таблицы 1. Так как, по условию задачи, $n=60$ и $\gamma =0,95$, то получим, что $q=0,188$.
Видим, что $q \[\left(S\left(1-q\right),S\left(1+q\right)\right)\] \[\left(0,4\cdot 0,812;0,4\cdot 1,188\right)=(0,3248;0,4752)\]
Ответ: $(0,3248;0,4752)$.
Пусть выборка имеет исправленное среднее квадратическое отклонение $S=0,9$. Пусть объем выборки $n=10$, а надежности равна $\gamma =0,999$. Найти доверительный интервал для оценки среднего квадратического отклонения данного распределения.
Решение:
Для начала найдем величину $q$ из таблицы 1. Так как, по условию задачи, $n=10$ и $\gamma =0,999$, то получим, что $q=1,8$.
Видим, что $q \[\left(0;S\left(1+q\right)\right)\] \[\left(0;0,9\cdot 2,8\right)=(0;;2,52)\]
Ответ: $(0;2,52)$.
Пусть выборка имеет исправленное среднее квадратическое отклонение $S=0,3$. Пусть объем выборки $n=30$, а надежности равна $\gamma =0,99$. Найти доверительный интервал для дисперсии данного распределения.
Решение:
Для начала найдем величину $q$ из таблицы 1. Так как, по условию задачи, $n=30$ и $\gamma =0,99$, то получим, что $q=0,43$.
Видим, что $q \[\left(S^2\left(1-q\right),S^2\left(1+q\right)\right)\] \[\left(0,09\cdot 0,57;0,09\cdot 1,43\right)=(0,0513;0,1287)\]
Ответ: $(0,0513;0,1287)$.











