Отображение плоскости на себя
Отображение плоскости на себя - это такое соответствие каждой точке плоскости какой-либо точки этой же плоскости, при котором каждая точка плоскость будет сопоставленной для какой-либо точки.
Примерами отображения плоскости на себя могут являться осевая симметрия (рис. 1,а) и центральная симметрия (рис. 1,б).
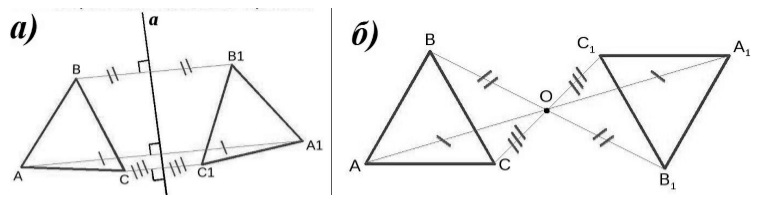
Рисунок 1. а) осевая симметрия; б) центральная симметрия
Понятие движения
Введем теперь определение движения.
Движением плоскости называется такое отображение плоскости на себя, при котором сохраняются расстояния (рис. 2).
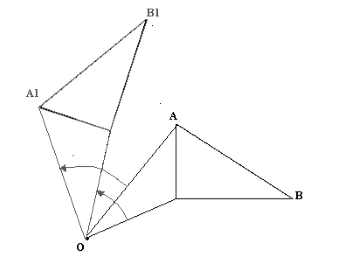
Рисунок 2. Пример движения
Теоремы, связанные с понятием движения
Доказательство.
Пусть нам дан отрезок $MN$. Пусть при заданном движении плоскости точка $M$ отображается на точку $M_1$ этой плоскости, а точка $N$ отображается на точку $N_1$ этой плоскости. Возьмем произвольную точку $P$ отрезка $MN$. Пусть она отображается в точку $\ P_1$ этой плоскости (рис. 3).
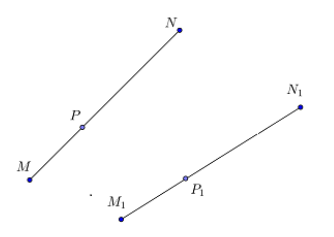
Рисунок 3. Отображение отрезка на отрезок при движении
Так как точка $P$ принадлежит отрезку $MN$, то выполняется равенство
Так как, по определению движения, расстояния сохраняются, то
Следовательно
Значит, точка $P_1$ лежит на отрезке $M_1N_1$. В силу произвольности выбора точки $P_1$ получаем, что отрезок $MN$ при движении отобразится на отрезок $M_1N_1$. Равенство же этих отрезков сразу вытекает из определения движения.
Теорема доказана.
При движении треугольник отображается на равный треугольник.
Доказательство.
Пусть нам дан треугольник $ABC$. По теореме 1, отрезок $AB$ переходит в отрезок $A_1B_1$, отрезок $AC$ переходит в отрезок $A_1C_1$, отрезок $BC$ переходит в отрезок $B_1C_1$, причем ${AB=A}_1B_1$, ${AC=A}_1C_1$, ${BC=B}_1C_1$. Следовательно, по III признаку равенства треугольников, треугольник $ABC$ переходит в равный ему треугольник $A_1B_1C_1$.
Теорема доказана.
Аналогично можно доказать, что луч отображается на луч, угол отображается на равный ему угол.
Для формулирования следующей теоремы вначале ведем следующее определение.
Наложением называется такое движение плоскости, которое обладает следующими аксиомами:
- Если при движении совпадают концы двух отрезков, то совпадают и сами отрезки.
- От начала любого луча можно отложить отрезок, равный данному отрезку и притом только один.
- В любую полуплоскость от любого луча можно отложить угол, равный данному неразвернутому углу, причем только один.
- Любая фигура является равной самой себе.
- Если фигура 1 равна фигуре 2, то и фигура 2 равна фигуре 1.
- Если фигура 1 равна фигуре 2, а фигура 2 равна фигуре 3, то фигура 1 равна фигуре 3.
Любое движение является наложением.
Доказательство.
Рассмотрим движение $g$ треугольника $ABC$. По теореме 2, при движении $g$ треугольник $ABC$ переход в равный ему треугольник $A_1B_1C_1$. По определению равных треугольников получаем, что существует наложение $f$, отображающее точки $A,B\ и\ C$ на точки $A_1,B_1\ и\ C_1$, соответственно. Докажем, что $g$ совпадает с $f$.
Предположим противное, что $g$ не совпадает с $f$. Тогда существует по крайней мере одна точка $M$, которая при движении $g$ переходит в точку $M_1$, а при наложении $f$ - в точку $M_2$. Так как, при $f$ и $g$ сохраняются расстояния, то имеем
То есть точка $A_1$ равноудалена от точек $M_1$ и $M_2$. Аналогично получим, что точки $B_1\ и\ C_1$ равноудалены от точек $M_1$ и $M_2$. Значит точки $A_1,B_1\ и\ C_1$ лежат на прямой, перпендикулярной к отрезку $M_1M_2$ и проходящей через его центр. Это не возможно, так как точки $A_1,B_1\ и\ C_1$ не лежат на одной прямой. Следовательно, движение $g$ совпадает с наложением $f$.
Теорема доказана.
Пример задачи на понятие движения
Доказать, что при движении угол отображается на равный ему угол.
Доказательство.
Пусть нам дан угол $AOB$. Пусть при заданном движении точки $A,\ O\ и\ B$ отображаются на точки $A_1,\ O_1\ и\ B_1$. По теореме 2 получаем, что треугольник $AOB$ отображается на треугольник $A_1O_1B_1$, причем эти треугольники равны между собой. Следовательно, $\angle AOB=\angle A_1O_1B_1$.












