Вероятность $P\left(X
Обозначение:
\[F\left(x\right)=P\left(XФункция распределения -- универсальная характеристика. Она существует для всех случайных величин -- и непрерывных и дискретных.Свойства функции распределения
- $F\left(x\right)$ - функция неубывающая, т.е. при $x_{1}
По теореме сложения вероятностей несовместных событий получим:
$F\left(x_{2} \right)-F\left(x_{1} \right)=P\left(x_{1} \le X
а поэтому
$F\left(x_{2} \right)-F\left(x_{1} \right)\ge 0$ или $F\left(x_{2} \right)\ge F\left(x_{1} \right)$,
что и требовалось доказать.
- Вероятность того, что случайная величина попадет на участок $\left[a;b\right)$, равна приращению интегральной функции распределения на этом участке.
Это утверждение следует непосредственно из первого свойства. Действительно, если положим $x_{1} =a,{\rm \; }x_{2} =b$, то получим:
Это свойство следует из того, что $\left(X
График функции распределения $F\left(x\right)$ есть график неубывающей функции, значения которой меняются от $0$ до $1$.
Геометрическое распределение
Пусть имеем независимое испытание Бернулли, в каждом из которых событие $A$ наступает с вероятностью $p,\ \ 0
Случайная величина $X$ означает количество испытаний, которые необходимо провести до первого появления события $A,$ она может принимать значения $0,\ 1,\ 2,\ \dots ,\ K,\ \dots ,\ $ вероятности этих значений: $P\left\{\xi =k\right\}={\left(1-p\right)}^k\cdot p.$
Вероятности для последовательных значений $K$ являют собой убывающую геометрическую прогрессию со знаменателем $q=1-q.$ Ряд распределения этой случайной величины $X$ имеет вид:
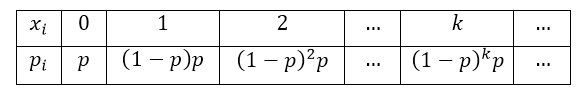
Рисунок 1.
Причем
Вычислим математическое ожидание:
и дисперсию:
Иногда рассматривают случайную величину $Y=X+1,$ которая равняется числу испытаний до получения результата $A.$ Ряд распределения величины $Y$ имеет вид:
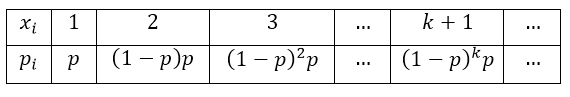
Рисунок 2.
Распределение случайной величины $Y=X+1$ будем называть «геометрическим распределением, что начинается с единицы».
Применение для решения задач
Пушка стреляет в цель до первого попадания. Вероятность попадания в цель $p=0,7.$ Найти закон распределения случайной величины $\xi -$количество выстрелов и вероятность того, что попадание наступит при четвертом выстреле.
Решение.
Закон распределения данной случайной величины будет иметь вид:

Рисунок 3.
В этом случае мы имели геометрическое распределение, что начинается с единицы.
Из орудия производится стрельба по цели до первого попадания. Вероятность попадания в цель $p = 0,6$. Найти вероятность того, что попадание произойдет при третьем выстреле.
Решение:
По условию $p = 0,6$, $q = 1 -- 0,6 = 0,4$, $k = 3$.
Искомая вероятность равна:
$P ( X = 3 ) = 0,4^2 \cdot 0,6 = 0,096$.












