Условным законом распределения одной из составляющих двумерной случайной величины $(X,Y)$ называется её закон распределения, вычисленный при условии, что другая составляющая принимает определенное значение или попадает в определенный интеграл.
Введем теперь по отдельности определения условного закона распределения для составляющей $X$ и для составляющей $Y$.
Условные законы распределения составляющих дискретной двумерной случайной величины
Пусть $(X,Y)$ - дискретная двумерная случайная величина.
Условным распределением составляющей $X$ при $Y=y$ называется совокупность условных вероятностей $p\left(x_1,y\right),\ p\left(x_2,y\right),..,p\left(x_n,y\right)$ при условии, что событие $Y=y$ уже произошло.
Если известен закон распределения двумерной случайной величины $(X,Y)$, то условная составляющая $X$ представляется в виде
Условным распределением составляющей $Y$ при $X=x$ называется совокупность условных вероятностей $p\left(x,y_1\right),\ p\left(x,y_2\right),..,p\left(x,y_m\right)$ при условии, что событие $X=x$ уже произошло.
Если известен закон распределения двумерной случайной величины $(X,Y)$, то условная составляющая $X$ представляется в виде
Условные законы распределения составляющих непрерывной двумерной случайной величины
Пусть $(X,Y)$ - непрерывная двумерная случайная величина.
Напомним, что для непрерывной случайной величины существует понятие плотности распределения случайной величины.
Условной плотностью $\varphi (x/y)$ распределения составляющей $X$ при $Y=y$ называется отношение плотности $\varphi (x,y)$ двумерной случайной величины $(X,Y)$ к плотности распределения $\varphi (y)$ при условии, что составляющая $Y$ приняла конкретное значение или попала в заданный интервал. То есть
\[\varphi (x/y)=\frac{\varphi (x,y)}{\varphi (y)}\]Условной плотностью $\varphi (y/x)$ распределения составляющей $Y$ при $X=x$ называется отношение плотности $\varphi (x,y)$ двумерной случайной величины $(X,Y)$ к плотности распределения $\varphi (x)$ при условии, что составляющая $X$ приняла конкретное значение или попала в заданный интервал. То есть
\[\varphi (y/x)=\frac{\varphi (x,y)}{\varphi (x)}\]Приведем еще две формулы для вычисления условных плотностей распределения. Если известна плотность совместного распределения, то условные плотности по составляющей $X$ и по составляющей $Y$ можно найти по формулам:
Введем несколько свойств для функций условной плотности распределения.
Свойство 1: Функции условной плотности распределения неотрицательны на всей области определения, то есть:
Свойство 2: Выполняются следующие равенства:
Условное математическое ожидание
Введем формулы для вычисления условных математических ожиданий для различных случаев.
- Условное математическое ожидание дискретной случайной величины $Y$ при $X=x$:
- Условное математическое ожидание дискретной случайной величины $X$ при $Y=y$:
- Условное математическое ожидание непрерывной случайной величины $Y$ при $X=x$:
- Условное математическое ожидание непрерывной случайной величины $X$ при $Y=y$:
Условное математическое ожидание $M(Y/X)$ называется функцией регрессии $X$ на $Y$.
Условное математическое ожидание $M(X/Y)$ называется функцией регрессии $Y$ на $X$.
Пример задачи на условное распределение
Распределение случайной величины задано таблицей.
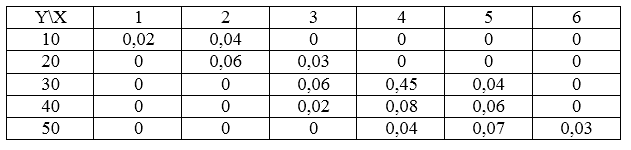
Рисунок 1.
Найти для этой двумерной случайной величины условное распределение по составляющей $X$, если $Y=10$.
Решение.
Для нахождения условного распределения по составляющей $X$, будем использовать следующую формулу:
\[p\left(x_i/y\right)=\frac{p\left(x_i,y\right)}{p(y)}\]Для начала необходимо найти ряд распределения случайной величины $Y$.
С помощью простейших вычислений, получим:

Рисунок 2.
Для нахождения условного распределения по составляющей $X$, будем использовать следующую формулу:
\[p\left(x_i/y\right)=\frac{p\left(x_i,y\right)}{p(y)}\]- Y=10
Получаем следующий ряд условного распределения по составляющей $X$:

Рисунок 3.











