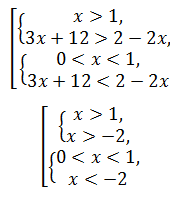Понятие неравенства с одной переменной
Неравенство вида $f(x) > (≥)g(x)$ будет называться неравенством с одной переменной.
Значение $x$, при котором выполняется неравенство из определения 1, называется корнем неравенства.
Если вспомнить курс лекций по математике и углубиться в тему «Дробно-рациональные неравенства», то можно изучить множество видов неравенств: линейные, тригонометрические, логарифмические, показательные… Приведем пример решения одного из таких неравенств с помощью построения совокупностей.
Решить $log_x(x+4)+log_x3 >log_x(2-2x)$
Решение.
Пользуясь свойством логарифма, получим
$log_x(3(x+4)) >lg(2-2x)$
$log_x(3x+12) >lg(2-2x)$
Данная система уравнений равносильна совокупности
Рисунок 1. Совокупность. Автор24 — интернет-биржа студенческих работ
Ответ: $(1,+∞)$.
Дробно-рациональные неравенства
Рассмотрим теперь понятие дробно-рационального неравенства.
Неравенство, которое имеет вид $\frac{P(x)}{Q(x)} >( ≥)0$ будем называть дробно рациональным неравенством.
Решение дробных неравенств, а также решение рациональных неравенств зачастую осуществляется методом промежутков (интервалов). В основе этого метода лежит следующий алгоритм решения.
Пусть нам дана функция $f(x)=\frac{(x-n)(x-m)}{(x-l)(x-k)}$, причем $n$
$x∈(-∞,n)$:
Используя неравенство (1), будем получать:
$(x-n)$
Четыре минуса, в общем, нам дадут плюсовое значение, то есть $f(x) >0$.
$x∈(n,m)$:
Используя неравенство (1) будем получать:
$(x-n) >0$, $(x-m)$
Три минуса, в общем, нам дадут минусовое значение, то есть $f(x)$
$x∈(m,l)$:
Используя неравенство (1) будем получать:
$(x-n) >0, (x-m) >0$, $(x-l)$
Два минуса, в общем, нам дадут плюсовое значение, то есть $f(x) >0$.
$x∈(l,k)$:
Используя неравенство (1) получим:
$(x-n) >0, (x-m) >0, (x-l) >0$, $(x-k)$
Один минус дает нам минусовое значение, то есть $f(x)$
$x∈(k,+∞)$:
Используя неравенство (1) будем получать:
$(x-n) >0, (x-m) >0, (x-l) >0, (x-k) >0$.
Все плюсы нам дадут плюсовое значение, то есть $f(x) >0$
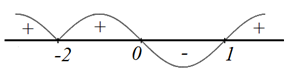
Это рассуждение можно иллюстрировать на числовой прямой (рис. 2).
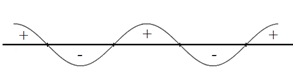
Рисунок 2. Числовая прямая. Автор24 — интернет-биржа студенческих работ
Эта иллюстрация называется кривой знаков и используется для решения рациональных и других неравенств $q(x) >( ≥)0$ методом промежутков.
Такое рассуждение справедливо для любого количества линейных множителей и в числителе, и в знаменателе. Также справедливо для случая, когда параметры не являются линейными. Поэтому из него можно вывести метод для решения большинства уравнений (и не только рациональных).
На самом деле знаки на такой кривой не всегда чередуются. К примеру, такое может быть при наличии в уравнение квадратного множителя.
Метод промежутков (интервалов)
- Вначале необходимо найти все корни уравнения $q(x)=0$ и части, в которых область определения имеет разрыв.
- И всех полученных в пункте $1$ числовых значений составляем кривую знаков для данного уравнения.
- Записываем ответ из кривой знаков, с учетом знака неравенства.
Пример решения рациональных и дробных неравенств методом промежутков.
Решить.
$\frac{(z-1)^7 (z+2)^4}{z≤ 0}$
Решение.
Решим для начала следующее уравнение и найдем точки разрыва ее области определения:
$\frac{(z-1)^7 (z+2)^4}{z}=0$
$(z-1)^7 (z+2)^4=0$
Корни: $z=1$ и $z=-2$
$z=0$-точка разрыва области определения.
Изобразим все полученные точки на числовой прямой и построим кривую знаков:
Рисунок 3. Кривая. Автор24 — интернет-биржа студенческих работ
Так как у нас знак неравенства «меньше или равно», то нам нужно выбрать промежуток со знаком минус, причем $1$ нужно включить в решение, а ноль (так как он не попадает в область определения) нет. Также необходимо не забыть значение $z=-2$.
Ответ: ${-2}∪(0,1]$.