Определение положительных и отрицательных чисел
Для определения положительных и отрицательных чисел воспользуемся координатной прямой, которая располагается горизонтально и направлена слева направо.
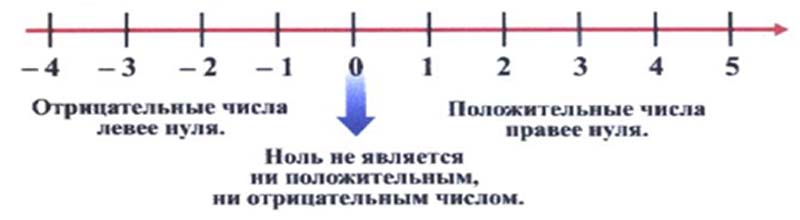
Началу отсчета на координатной прямой соответствует число нуль, которое не относится ни к положительным, ни к отрицательным числам.
Числа, соответствующие точкам координатной прямой, которые лежат правее от начала отсчета, называются положительными.
Числа, соответствующие точкам координатной прямой, которые лежат левее от начала отсчета, называются отрицательными.
Из данных определений вытекает, что множество всех отрицательных чисел противоположно множеству всех положительных чисел.
Отрицательные числа всегда записывают со знаком «–» (минус).
Примеры положительных чисел:
- Натуральные числа $3$, $13$, $333$, $578$, $10456$ и т.д.
- Рациональные числа $\frac{9}{17}$, $4 \frac{11}{23}$, $5,25$, $4,(79)$.
- Иррациональные числа $π$, $е$, $\sqrt[3]{2}$, бесконечная непериодическая десятичная дробь $103,1012341981…$
Все натуральные числа являются положительными.
Примеры отрицательных чисел:
- Рациональные числа $-\frac{9}{17}$, $-4 \frac{11}{23}$, $–5,25$, $–4,(79)$.
- Иррациональные числа$ -\sqrt[3]{2}$, бесконечная непериодическая десятичная дробь $–103,1012341981…$
Для упрощения записи перед положительными числами часто не записывают знак «+» (плюс), а перед отрицательными знак «–» записывают всегда. В подобных случаях необходимо помнить, что запись «$17,4$» равносильна записи «$+17,4$», запись «$\sqrt{5}$» равносильна записи «$+\sqrt{5}$» и т.д.
Таким образом, можно использовать следующее определение положительных и отрицательных чисел:
Числа, записанные со знаком «+», называются положительными, а со знаком «–» – отрицательными.
Используется определение положительных и отрицательных чисел, которое основано на сравнении чисел:
Положительными числами являются числа больше нуля, а отрицательными числами – числа меньше нуля.
Таким образом, число нуль разделяет положительные и отрицательные числа.
Правила чтения положительных и отрицательных чисел
При чтении числа со знаком впереди него сначала читается его знак, а затем само число.
Например, «$+17$» читают «плюс семнадцать»,
«$-3 \frac{4}{11}$» читают «минус три целых четыре одиннадцатых».
Стоит отметить, что названия знаков «плюс» и «минус» не склоняются, в то время как числа могут склоняться.
Например, «$x=-18$» можно читать как «икс равен минус восемнадцать», так и «икс равен минус восемнадцати».
Интерпретация положительных и отрицательных чисел
Положительные числа используются для обозначения увеличения какой-нибудь величины, прихода, прибавки, возрастание значения и т.д.
Отрицательные числа применяют для противоположных понятий – для обозначения уменьшения какой-нибудь величины, расхода, недостатка, долга, снижения значения и т.д.
Рассмотрим примеры.
Читатель взял в библиотеке $4$ книги. Положительное значение числа $4$ показывает число книг, которые есть у читателя. Если ему нужно сдать $2$ книги в библиотеку, можно использовать отрицательное значение $–2$, которое будет указывать на уменьшение числа книг у читателя.
Положительные и отрицательные числа часто используют для описания значений различных величин в измерительных приборах. Например, термометр для измерения температуры имеет шкалу, на которой отмечены положительные и отрицательные значения.
Похолодание на улице на $3$ градуса, т.е. снижение температуры, можно обозначить значением $–3$, а повышение температуры на $5$ градусов – значением $+5$.
Принято отрицательные числа изображать синим цветом, что символизирует холод, низкую температуру, а положительные числа – красным цветом, что символизирует тепло, высокую температуру. Обозначение положительных и отрицательных чисел с помощью красного и синего цвета используется в различных ситуациях для выделения знака чисел.