Сложение и вычитание
Практически все арифметические операции в компьютере сводятся к операции сложения.
Разберем все возможные случаи, используя $2$ числа: $A$ и $B$. Заметим, что все операции сложения чаще всего ведутся в обратных кодах. Напомним, что у положительного числа все коды одинаковы.
Основные принципы сложения в двоичной системе счисления:
При сложении в столбик применяются те же правила, что и при сложении десятичных чисел.
Сложение в обратных кодах
Случай 1. $A$ и $B$ -- положительные числа.
При сложении таких чисел просто суммируются их обратные коды (для положительных чисел они равны прямым), включая знаковый разряд. Т.к. знаковый разряд у положительных чисел равен $0$, то у суммы он также равен $0$, таким образом, число также будет положительным.

Рисунок 1.
Случай 2. $A$ -- положительное, $B$ -- отрицательное, по модулю больше $A$.
В этом случае числа $A$ и $B$ (для отрицательного числа берется обратный код) просто складываются и получается результат в обратном коде:

Рисунок 2.
Для перевода результата в прямой код биты цифровой части инвертируются: $1000 \ 1010=-10$.
Случай 3. $A$ -- положительное, $B$ -- отрицательное, по модулю меньше $A.$
Если в этом случае поступить таким же образом, то получим ошибку расчета. Компьютер решает эту проблему переносом получившейся «лишней единицы» из знакового разряда в младший разряд получившейся суммы. Не забываем для отрицательного числа $A$ записать обратный код:

Рисунок 3.
Случай 4. $A$ и $B$ -- отрицательные.
В этом случае во избежание ошибки снова нужно будет перенести единицу из знакового разряда в младший разряд числа.

Рисунок 4.
При сложении чисел возможен вариант переполнения, когда полученный результат не помещается в выделенное для него место в памяти.
Самый надежный способ проверки не произошло ли переполнение -- проверка знака результата. Если он получается не таким, какой должен быть, значит произошло переполнение.
Максимально возможное значение по модулю для чисел со знаком равно $2^{n-1}$, где n -- количество бит для хранения числа.
Например, если на хранение числа отводится $1$ байт, то максимально возможное значение по модулю $2^{8-1}=2^7=128$. Если число по модулю получается больше, то для операции необходимо выделить больше памяти.
Заметим, что переполнение возможно в случае, когда числа имеют одинаковый знак (оба положительны или оба отрицательны).
Случай 5. Переполнение, когда $A$ и $B$ -- положительные.

Рисунок 5.
Мы получили в результате сложения двух положительных чисел -- отрицательное. Т.е. произошло переполнение. Ситуация решается расширением диапазона:
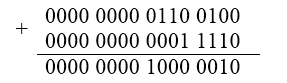
Рисунок 6.
Случай 6. Переполнение, когда $A$ и $B$ -- отрицательные.
Ситуация такая же, как и в случае $5$. Решается тем же способом -- расширением диапазона.
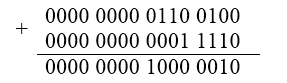
Рисунок 7.
Сложение в дополнительных кодах
Случай $1$. $A$ и $B$ -- положительные.
Стандартный случай, т.к. у положительных чисел прямой, обратный и дополнительный коды совпадают.
Случай $2$. $A$ -- положительное, $B$ -- отрицательное, по модулю больше $A$.
В случае использования дополнительных кодов получим сразу правильный результат, в отличие от сложения обратных кодов.
Случай $3$. $A$ -- положительное, $B$ -- отрицательное, по модулю меньше $A$.
В отличие от сложения обратных кодов, где нужно было прибавлять «лишнюю» единицу к полученному коду, в этом случае нужно ее просто отбросить.
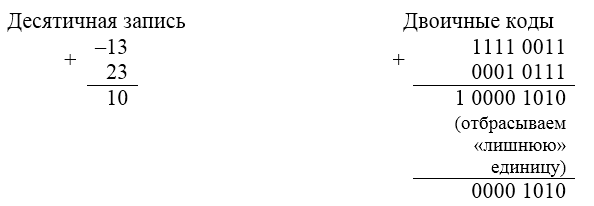
Рисунок 8.
Случай $4$. $A$ и $B$ -- отрицательные.
В этом случае тоже отбрасываем «лишнюю» единицу.
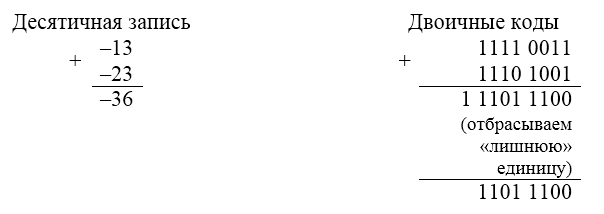
Рисунок 9.
Случай $5$ и $6$. Переполнение -- аналогично обратному.
При необходимости выполнения вычитания чисел, оно сводится к сложению отрицательных чисел. Например, $A-B=A+(-B).$
Умножение
Т.к. умножение - сложная операция, то специально для нее в компьютере имеется регистр (накапливающий сумматор) и с помощью последовательности сдвигов и сложений получается результат.
Умножение в двоичной системе выполняется быстрее, чем сложение и вычитание, т.к. сложение можно производить в прямом коде.
Для определения знака результата умножения над знаковыми разрядами совершается операция сложения по модулю («строгое (исключающее) ИЛИ» или «XOR»).
Умножим числа $-13$ и $23$:

Рисунок 10.
Для удобства умножения нули между знаковым разрядом и первой цифрой числа за писывать не будем.
Полученный результат содержит $10$ цифр. Приведем его к виду из $16$ бит, добавив нули между знаковым разрядом и модулем числа:
$1000 \ 0001 \ 0010 \ 1011.$
Деление
Деление для компьютера является трудной операцией. Обычно оно реализуется путем многократного прибавления к делимому дополнительного кода делителя.
Рассматривая операцию деления, как и в случае деления десятичных чисел, необходимо выделить $3$ варианта выполнения деления:
-
деление без остатка;
-
деление с остатком;
-
деление с заданной точностью.













