Перпендикулярные прямые
Перпендикулярными прямыми называются прямые, которые располагаются на одной плоскости и пересекаются под прямым углом.
Прямой угол равен $90^о$.
Перпендикулярными могут быть не только прямые, но и лучи, и отрезки.
Рассмотрим прямоугольник и квадрат. В них все углы прямые, т.е. равны 90о. Следовательно, соседние стороны каждой и этих геометрических фигур перпендикулярны между собой.
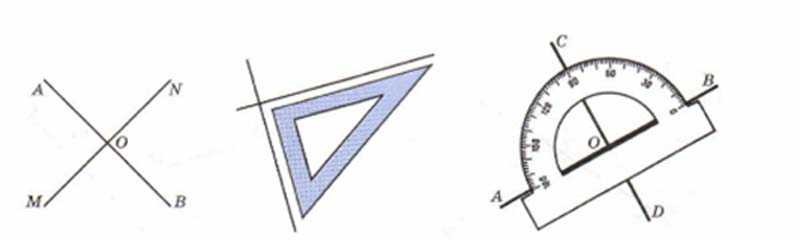
Для построения прямого угла, например, в школьной тетради, можно использовать чертежный треугольник, у которого один из углов равен $90^\circ$. Также можно воспользоваться транспортиром: провести ровную линию, отметить точку возле цифры $90$ и построить проекцию из этой точки на проведенную прямую. Самый простой способ – нарисовать перпендикулярные прямые по клеточкам в тетради, т.к. они имеют форму квадрата со сторонами, которые располагаются под прямым углом.
Прямые, которые пересекаются под прямым углом, называются перпендикулярными прямыми.
Перпендикулярные прямые сокращенно в математике обозначают с помощью специального знака «\perp». Например, тот факт, что прямая $AB$ перпендикулярна относительно прямой $MN$ записывается как $AB \perp MN$.
Если $AB \perp MN$, то $MN \perp AB$.
Отрезки (или лучи), которые лежат на перпендикулярных прямых, называются перпендикулярными отрезками (или лучами).
Параллельные прямые
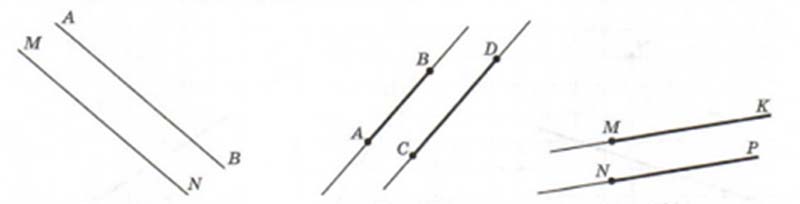
Представим плоскость, на которой проведена одна прямая линия. Назовем ее $AB$. На этой же плоскости вне прямой отмечена точка $C$. Через эту точку $C$ можно провести бесконечное количество прямых, но только одна из них (назовем ее $CD$) никогда не пересечется с прямой $AB$. Говорят, что прямая $AB$ параллельна относительно прямой $CD.$
Сформулируем определение параллельных прямых:
Параллельными прямыми называются две прямые, которые расположены на плоскости и не пересекаются.
Сформулируем еще и правило:
Через точку, которая не принадлежит на прямой, можно провести только одну прямую, которая будет параллельна исходной.
В жизни параллельные прямые можно встретить, например, на прямых участках железнодорожных путей или прямых участках трамвайных путей.
Довольно часто параллельные прямые встречаются в геометрических фигурах. Например, противоположные стороны квадрата, прямоугольника, параллелограмма, основания трапеции.
Такие геометрические фигуры, как квадрат и прямоугольник, интересны тем, что они содержат и перпендикулярные, и параллельные стороны.
Таким образом, две любые прямые на плоскости могут или пересекаться в одной точке, или не пересекаться.
Параллельные прямые сокращенно в математике обозначают с помощью специального знака «\parallel». Например, тот факт, что прямая $AB$ параллельна прямой $MN$ записывается как $AB \parallel MN$.
Если $AB \parallel MN$, то $MN \parallel AB$.
Отрезки (или лучи), которые лежат на параллельных прямых, называются параллельными отрезками (или лучами).
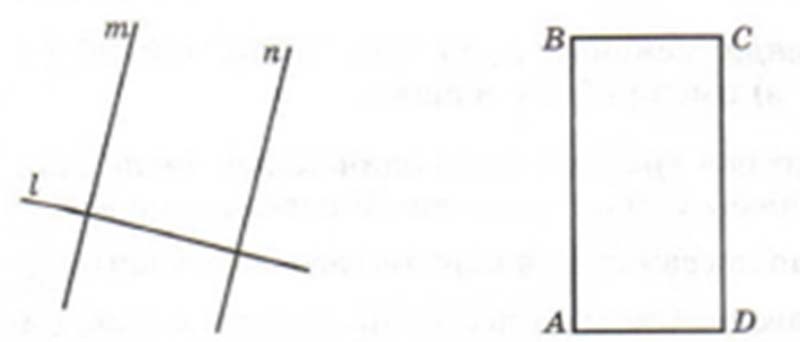
Рассмотрим квадрат $ABCD$.
Его стороны $AB$ и $CD$, $BC$ и $DA$ – попарно параллельные.
Стороны $AB$ и $BC$, $BC$ и $CD$, $CD$ и $DA$, $DA$ и $AB$ – попарно перпендикулярные.
Если представить любые две прямые, которые находятся в одной плоскости, такие, что они перпендикулярны третей прямой, следовательно, эти прямые параллельные между собой.
Прямые $m$ и $n$ на рисунке перпендикулярны прямой $l$. Они параллельны друг другу.
В прямоугольнике противоположные стороны параллельны и образуют прямые углы с другими сторонами этого прямоугольника.
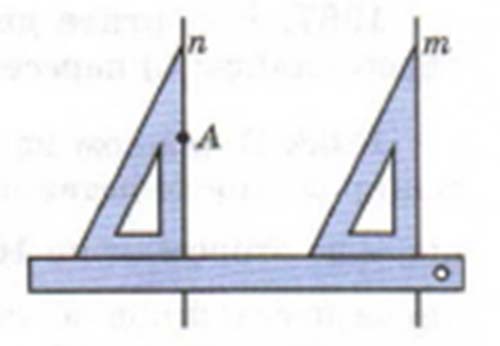
Для построения параллельных прямых можно использовать треугольник и линейку. На рисунке показано, как с помощью чертежных приборов можно начертить прямую $n$, которая проходит через точку $A$ параллельно прямой $m$.