Параметрический способ задания функций
Пусть даны два уравнения
$x=\phi (t)$ и $y=\psi (t)$
В которых $t$ принимает значения с отрезка [n1; n2]. Каждому значению t соответствуют значения x и y -- координаты точки на плоскости Оxy.
Когда $t$ изменяет свое значение на промежутке от $n1$ до $n2$, точка описывает некоторую кривую. Уравнения $x=\phi (t)$ и $y=\psi (t)$ получили название параметрических для кривой, а $t$ -- параметра.
Предположим, что функция $x=\phi (t)$ имеет обратную функцию $t=\ (x)$. Тогда справедливо равенство:
Параметрический способ задания функций широко применяется в механике. Так, если в плоскости некоторая материальная точка находится в движении (время $t$), и законы движения проекций этой точки на оси координат известны:
Уравнения являются параметрическими уравнениями траекторий движущейся точки. Исключая временной параметр, получим уравнение траектории в форме $y = f(x)$.
Определить траекторию и место падения груза, сброшенного с самолета, движущегося горизонтально со скорость $v_0$ на высоте $y_0$.
Решение.
Допустим, что груз сбрасывается с момент пересечения самолетом оси Oy. Тогда очевидно, что горизонтальное перемещение груза равномерно и имеет постоянную скорость:
$x = v_0 t$
А вертикальное перемещение:
\[s=\frac{gt^{2} }{2} \]Следовательно, расстояние от груза до земли в произвольный момент падения:
\[y=y_{0} -\frac{gt^{2} }{2} \]Уравнения горизонтального и вертикального перемещения тела являются параметрическими. Для того, чтобы исключить временной параметр $t$, найдем его значение из первого уравнения.
\[t=\frac{x}{v_{0} } \]Полученное выражение подставим во второе параметрическое уравнение чтобы найти уравнение траектории:
\[y=y_{0} -\frac{g}{2v_{0}^{2} } x^{2} \]Откуда:
\[x=v_{0} \sqrt{\frac{2y_{0} }{g} } \]Уравнения некоторых кривых в параметрической форме:
- Окружность
- Гипербола
Уравнение окружности имеет вид:
\[x^{2} +y^{2} =r^{2} \]Параметрические кривые окружности:
\[\begin{array}{l} {x=r\cos t} \\ {y=r\sin t} \end{array}\]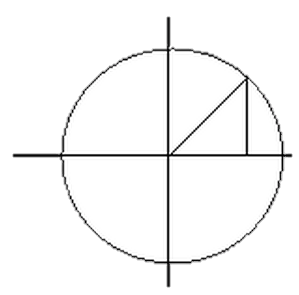
Рисунок 1. Окружность и ее параметрические кривые
Уравнение гиперболы имеет вид:
\[\frac{x^{2} }{a^{2} } -\frac{y^{2} }{b^{2} } =1\]Параметрические кривые гиперболы:
\[\begin{array}{l} {\left|x\right|=a\cdot cht} \\ {y=b\cdot cht} \end{array}\]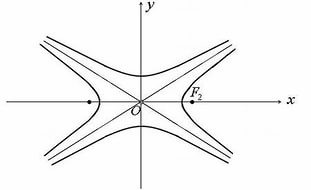
Рисунок 2. Гипербола и ее параметрические кривые
Записать уравнение окружности в параметрическом виде.
\[x^{2} +y^{2} =36\]Решение.
- Представим уравнение окружности в виде: \[x^{2} +y^{2} =r^{2} \] \[x^{2} +y^{2} =6^{2} \]
- Параметрические кривые окружности: \[\begin{array}{l} {x=r\cos t} \\ {y=r\sin t} \end{array}\] \[\begin{array}{l} {x=6\cos t} \\ {y=6\sin t} \end{array}\]
Значит, радиус $r$ равен 6.
Записать уравнение гиперболы в параметрическом виде.
\[\frac{x^{2} }{25} -\frac{y^{2} }{9} =1\]Решение.
- Представим уравнение гиперболы в виде: \[\frac{x^{2} }{5^{2} } -\frac{y^{2} }{3^{2} } =1\]
- Параметрические кривые гиперболы: \[\begin{array}{l} {\left|x\right|=5\cdot cht} \\ {y=3\cdot cht} \end{array}\]












