Геометрический и механический смысл производной
Для начала вспомним определение производной функции в точке.
Если существует конечный предел отношения приращения функции $f(x)$ в точке $x_0$ к приращению аргумента $\triangle x$, при $\triangle x\to 0$, то он называется производной функции $f(x)$ в точке $x_0$.
\[{\mathop{lim}_{\triangle x\to 0} \frac{f\left(x_0+\triangle x\right)-f\left(x_0\right)}{\triangle x}\ }={\mathop{lim}_{\triangle x\to 0} \frac{\triangle y}{\triangle x}\ }\]Производная имеет геометрический и механический смысл. Рассмотрим их подробнее.
Геометрический смысл производной
Рассмотрим геометрический смысл понятия производная (рис. 1).
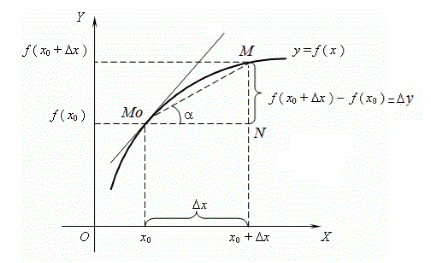
Пусть функция $f(x)$ дифференцируема в точке $x_0\in X$. Рассмотрим точку $M_0(x_0,f\left(x_0\right))\in f(x)$. Придадим $x_0$ приращение $\triangle x$, получим точку
$M(x_0+\triangle x,f\left(x_0+\triangle x\right))\in f(x)$. Мы видим, что
То есть $\left|MN\right|$ - приращение данной функции. Очевидно, что $\frac{\triangle y}{\triangle x}=tg\alpha $
Где $\alpha $ - угол наклона касательной к графику функции $f(x)$ в точке $M_0$.
Таким образом, геометрический смысл производной представляет собой угловой коэффициент касательной функции $f(x)$ в точке $x_0$. Иначе также -- это тангенс угла наклона касательной к графику данной функции.
Механический смысл производной
Механический смысл производной состоит в следующем: скорость материальной очки в момент времени $t$ есть производная пути по времени в этот момент.
Также можно отметить, что ускорение материальной точки в момент времени $t$ есть производная скорости по времени в данный момент времени.
Задачи на приложение производной
На рисунке изображён график функции $y=f(x)$ и касательная к нему в точке с абсциссой $x_0$. Найдите значение производной функции $f(x)$ в точке $x_0$.
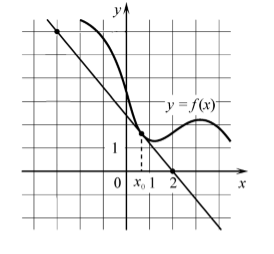
Рисунок 2.
Решение.
Так как по геометрическому смыслу производной $f'\left(x_0\right)=tg\alpha $, то нам нужно найти тангенс угла наклона касательной. Рассмотрим рисунок:
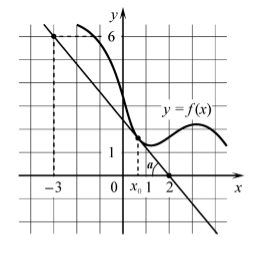
Рисунок 3.
Получаем: $f'\left(x_0\right)=tg\alpha =\frac{6}{5}=1,2$
Ответ: $1,2$.
На рисунке изображён график функции $y=f(x)$ и касательная к нему в точке с абсциссой $x_0$. Найдите значение производной функции $f(x)$ в точке $x_0$.
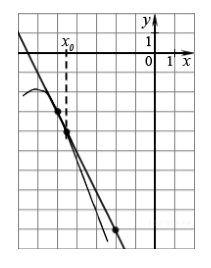
Рисунок 4.
Решение.
Так как по геометрическому смыслу производной $f'\left(x_0\right)=tg\alpha $, то нам нужно найти тангенс угла наклона касательной. Рассмотрим рисунок:
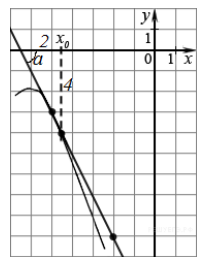
Рисунок 5.
Здесь нужно также отметить, что на самом деле угол между касательной и направлением оси $Ox$ тупой, следовательно, нам необходимо принять производную со знаком «минус». Получаем: $f'\left(x_0\right)=-tg\alpha =-\frac{2}{4}=-\frac{1}{2}$
Ответ: $-\frac{1}{2}$.
Материальная точка движется по закону
\[x\left(t\right)=5t^4+2t^3-3t+7,\]где $x$ - расстояние от начала движения в метрах, $t$ - время в секундах. Требуется найти скорость и ускорение материальной точки в момент времени $t=2c$.
Решение:
Так как $x$ - расстояние от начала движения в метрах, а $t$ - время в секундах, уравнение $x\left(t\right)=5t^4+2t^3-3t+7$ задает расстояние материальной точки от начала движения в зависимости от текущего времени.
Для нахождения скорости используем механический смысл производной.
Найдем первую производную:
\[{v\left(t\right)=x}'(t)={\left(5t^4+2t^3-3t+7\right)}'=20t^3+6t^2-3\]Найдем значение скорости при $t=2c$.
\[v\left(2\right)=20\cdot 8+6\cdot 4-3=160+24-3=181\ м/с\]Для нахождения ускорения используем дополнение к механическому смыслу производной.
Найдем первую производную от скорости:
\[{a\left(t\right)=v}'\left(t\right)={\left(20t^3+6t^2-3\right)}'=60t^2+12t\]Найдем значение ускорения при $t=2c$.
\[a\left(2\right)=60\cdot 4+12\cdot 2=240+24=264\ м/с^2\]











