Точкой разрыва функции называется такая точка а, в которой функция не является непрерывной.
На рисунке 1 изображена непрерывная функция, а на рисунке 2 -- функция, имеющая разрыв в точке а.
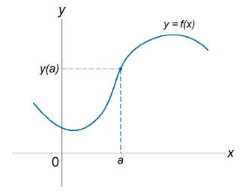
Рисунок 1. Непрерывная функция
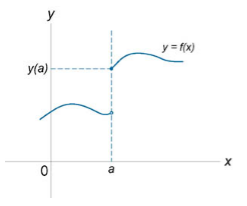
Рисунок 2. Точка разрыва функции
Таким образом, условие непрерывности не должно выполняться:
\[\mathop{\lim }\limits_{x\to a} f(x)\ne f(a)\]Данное условие справедливо для устранимой точки разрыва
Определить точку разрыва функции
\[f(x)=\frac{\sin x}{x} \]Решение:
- Найдем область определения данной функции: \[D(f)=\left(-\infty ;0\right)\cup (0;+\infty )\]
- Из области определения видно, что в точке х = 0 функция не определена \[f(x)=\frac{\sin x}{x} =1\ne f(0)=\frac{\sin x}{x} \]
Вывод: Функция имеет устранимую точку разрыва x = 0
Точка а = х называется неустранимой точкой разрыва первого рода (рис.3), если выполняется условие:
\[\mathop{\lim }\limits_{x\to a-0} f(x)\ne \mathop{\lim }\limits_{x\to a+0} f(x)\ne f(a)\]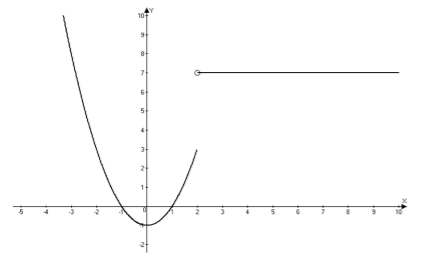
Рисунок 3.Точка разрыва первого рода
Определить разрыв функции
\[f(x)=\left\{\begin{array}{cc} {x,} & {x\le 1} \\ {\ln x,} & {x>1} \end{array}\right. \]Решение:
\[\mathop{\lim }\limits_{x\to 1+0} f(x)=\mathop{\lim }\limits_{x\to 1+0} \ln x=0\] \[\mathop{\lim }\limits_{x\to 1-0} f(x)=\mathop{\lim }\limits_{x\to 1} x=1\] \[\mathop{\lim }\limits_{x\to 1-0} f(x)\ne \mathop{\lim }\limits_{x\to 1+0} f(x)\]Вывод: В точке 1 функция имеет разрыв первого рода.
Точка а = х называется неустранимой точкой разрыва второго рода (рис.4), если хотя бы один из односторонних пределов не существует или равен бесконечности.
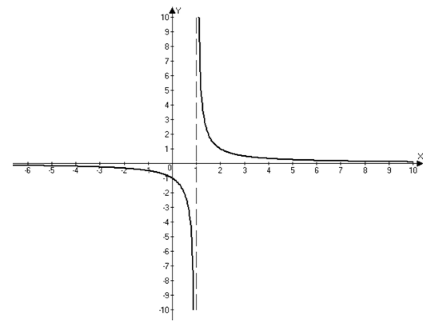
Рисунок 4.Точка разрыва второго рода
Определить вид точки разрыва
\[f(x)=tgx\]Решение:
\[\mathop{\lim }\limits_{x\to \frac{\pi }{2} +\pi k+0} tgx=-\infty \] \[\mathop{\lim }\limits_{x\to \frac{\pi }{2} +\pi k-0} tgx=+\infty \]Вывод: Точка $\frac{\pi }{2} +\pi k$ - точка разрыва второго рода












