Непрерывность функции в точке
Существует примерно четыре определения непрерывности функции в точке.
Функция $f(x)$ называется непрерывной в точке $х=х_0$, если $\forall \varepsilon >{\rm 0}$ $\exists \delta (\varepsilon ,E_{0} ) >{\rm 0}$такое, что $\left|f(x)-f(x_{0} )\right|
Это определение непрерывности функции в точке эквивалентно определению предела функции в точке, с той лишь разницей, что значение предела равно значению функции в этой точке, т. е. $\mathop{{\rm lim\; }}\limits_{{\rm x}\to {\rm x}_{{\rm 0}} } f(x)=f(x_{0} )$.
Функция $f(x)$ непрерывна в точке $х=х_0$, если $\mathop{{\rm lim\; }}\limits_{{\rm x}\to {\rm x}_{{\rm 0}} } f(x)=f(x_{0} )$.
Тот факт, что $\exists $$\mathop{{\rm lim\; }}\limits_{{\rm x}\to {\rm x}_{{\rm 0}} } f(x)=f(x_{0} )$ эквивалентен f$(x_0+0)=f(x_0-0)=f(x_0)$.
Введём в рассмотрение $\Delta y(x_0)=f(x_0+ \Delta x)=f(x_0)$, $\Delta x$ - приращение аргумента, $\Delta y(x_0)$ - приращение функции. Функция $f(x)$ называется непрерывной в точке $х_0$, если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.
Если в какой-то точке какое-либо определение (1 - 4) нарушено, то функция $f(x)$ называется разрывной в этой точке.
Возможны такие случаи:
1.${\rm f(x}_{{\rm 0}} +0)\ne f(x_{0} -0)\ne f(x_{0} )$ - в этом случае $х=х_0$ - точка разрыва.
2.${\rm f(x}_{{\rm 0}} +0)=f(x_{0} )\ne f(x_{0} -0)$ - функция $f(x)$ называется непрерывной справа или ${\rm f(x}_{{\rm 0}} +0)=\mathop{\lim }\limits_{x\to x_{0} +0} f(x)=f(x_{0} )$
3.${\rm f(x}_{{\rm 0}} -0)=f(x_{0} )\ne f(x_{0} +0)$ - функция $f(x)$ называется непрерывной слева или ${\rm f(x}_{{\rm 0}} -0)=\mathop{\lim }\limits_{x\to x_{0} -0} f(x)=f(x_{0} )$.
Пусть функции $f(x)$ и $g(x)$ непрерывны в точке $х=а$, тогда $f(x) \pm g(x)$, ${\rm f}{\rm (x)}\cdot {\rm g(x)}$, $\frac{f(x)}{g(x)} $, если $g(а) \ne 0$ непрерывны в точке $х=а$.
Доказательство.
Т. к. функции $f(x)$ и $g(x)$ непрерывны в точке $х=а$, то $\mathop{{\rm lim\; }}\limits_{{\rm x}\to {\rm 0}} f(x)=f(0)$ и $\mathop{{\rm lim\; }}\limits_{{\rm x}\to {\rm 0}} {\rm g}(x)=g(0)$, тогда по свойству пределов:
Следовательно, сумма и разность непрерывных функций являются непрерывными.
Теоремы, связанные с понятием непрерывности
Теорема Больцано-Коши (1)
Если функция $f(x)$ непрерывна на отрезке $[a,b]$ и на его концах принимает значения разных знаков, то между $a\ и\ b$ существует по крайней мере одна точка $c$ такая, что $f\left(c\right)=0$.
Теорема Больцано-Коши (2)
Если функция $f(x)$ непрерывна на отрезке $[a,b]$ и на его концах принимает различные значения $f\left(a\right)=A\ne f\left(b\right)=B$, то для любого действительного числа $C$, лежащего между $A\ и\ B$, существует по крайней мере одна точка $c$, лежащая между $a\ и\ b$, такая, что $f\left(c\right)=C$.
Теорема о существовании обратной непрерывной функции
Если возрастающая (убывающая) функция $f(x)$ непрерывна на промежутке $X\in R$, то в промежутке $y=E(f)\in R$ у нее существует обратная функция, которая также возрастает (убывает) и непрерывна в своей области определения.
Теорема Вейерштрасса (1)
Если функция $f(x)$ непрерывна на отрезке $[a,b]$, то она ограничена на этом отрезке (снизу и сверху).
Теорема Вейерштрасса (2)
Если функция $f(x)$ непрерывна на отрезке $[a,b]$, то она достигает свою точную верхнюю и нижнюю границы.
Точки разрыва функции
Точки разрыва делятся на два рода: точки разрыва первого и второго рода. Причем точки разрыва первого рода, в свою очередь, подразделяется на точки устранимого разрыва и точки разрыва с конечным скачком.
Точка $x_0\in X$ называется точкой разрыва первого рода, если в ней существую конечные пределы ${\mathop{lim}_{x\to x_0-0} f(x_0)\ }$, ${\mathop{lim}_{x\to x_0+0} f(x_0)\ }$, но нарушается равенство ${\mathop{lim}_{x\to x_0-0} f(x_0)\ }={\mathop{lim}_{x\to x_0+0} f(x_0)\ }=f(x_0)$
Точка $x_0\in X$ называется точкой устранимого разрыва, если она является точкой разрыва первого рода и выполняется ${\mathop{lim}_{x\to x_0-0} f(x_0)\ }={\mathop{lim}_{x\to x_0+0} f(x_0)\ }\ne f(x_0)$
Точка $x_0\in X$ называется точкой разрыва с конечным скачком, если она является точкой разрыва первого рода и выполняется ${\mathop{lim}_{x\to x_0-0} f(x_0)\ }\ne {\mathop{lim}_{x\to x_0+0} f(x_0)\ }$
При этом число ${\mathop{lim}_{x\to x_0+0} f(x_0)\ }-{\mathop{lim}_{x\to x_0-0} f(x_0)\ }$ называется скачком функции.
Точка $x_0\in X$ называется точкой разрыва второго рода, если в ней хотя бы один из пределов ${\mathop{lim}_{x\to x_0-0} f(x_0)\ }$, ${\mathop{lim}_{x\to x_0+0} f(x_0)\ }$ бесконечен или не существует.
Задачи на исследование непрерывности функции
Исследовать на непрерывность функцию
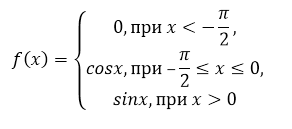
Рисунок 1.
Решение:
Очевидно, мы имеет две точки, подозрительные на разрыв:
- $x=-\frac{\pi }{2}$
Значит, выполняется равенство ${\mathop{lim}_{x\to x_0-0} f(x_0)\ }={\mathop{lim}_{x\to x_0+0} f(x_0)\ }=f(x_0)$, следовательно, функция непрерывна.
- $x=0$
Значит, пределы конечны и выполняется ${\mathop{lim}_{x\to x_0-0} f(x_0)\ }\ne {\mathop{lim}_{x\to x_0+0} f(x_0)\ }$, следовательно, функция имеет точку разрыва первого рода с конечным скачком.
Скачек функции равен:
\[0-1=-1\]












