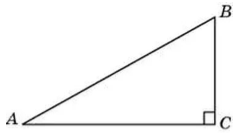
Будем рассматривать прямоугольный треугольник $ABC$ c прямым углом $C$ (рис. 1).
 треугольник">
треугольник">
Рисунок 1. Прямоугольный треугольник
Будем рассматривать угол $A$. Тогда катет $BC$ будет называться противолежащим катетом, а катет $AC$ прилежащим к углу $A$.
Синус, косинус, тангенс и котангенс острого угла прямоугольного треугольника
Введем определения синуса, косинуса, тангенса и котангенса острого угла прямоугольного треугольника.
Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе данного треугольника.
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе данного треугольника.
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету данного треугольника.
Синусом острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему катету данного треугольника.
То есть, имеем:
Из формул (1) и (2) очевидно, что
Проверим теперь следующее тождество:
Подставим формулы (1) и (2), получим
Из теоремы Пифагора мы знаем, что ${BC}^2+{AC}^2={AB}^2$, следовательно
Тождество (5) называется основным тригонометрическим тождеством.
Основные значения синуса, косинуса, тангенса и котангенса острого угла прямоугольного треугольника
Вычислим значения синуса, косинуса, тангенса и котангенса для ${30}^{{}^\circ },\ {45}^{{}^\circ }$ и ${60}^{{}^\circ }$. Для этого вспомним следующую теорему.
Катет прямоугольного треугольника, лежащий напротив угла в ${30}^{{}^\circ }$, равняется половине гипотенузы этого треугольника.
Пусть для начала у нас $\angle A={30}^{{}^\circ }$. Так как треугольник прямоугольный, то $\angle B={60}^{{}^\circ }$.
По теореме 1, имеем $AB=2BC$.
Используя основное тригонометрическое тождество (5), получим:
Теперь нетрудно найти тангенсы и котангенсы этих углов.
Пусть теперь $\angle A={45}^{{}^\circ }$. Тогда $\angle B={45}^{{}^\circ }$, то есть прямоугольный треугольник -- равнобедренный. По теореме Пифагора ${BC}^2+{AC}^2={AB}^2$, следовательно, ${AB}^2={2BC}^2=2{AC}^2$, то есть
Тогда
Сведем все полученные данные в таблицу (таблица 1).

Рисунок 2. Основные значения синусов, косинусов, тангенсов и котангенсов
Пример задачи на нахождение синуса, косинуса, тангенса и котангенса острого угла прямоугольного треугольника.
Найти значение синуса, косинуса, тангенса и котангенса угла $A$, если $AB=5,\ BC=4,\ AC=3.$
Решение.
Все решение задачи будем производить с помощью определений 1-4. Получим:
\[sinA=\frac{BC}{AB}=\frac{4}{5}=0,8\] \[cosA=\frac{AC}{AB}=\frac{3}{5}=0,6\] \[tgA=\frac{BC}{AC}=\frac{4}{3}=1\frac{1}{3}\] \[ctgA=\frac{AC}{BC}=\frac{3}{4}=0,75\]










