Прямую $с$ называют секущей для прямых $а$ и $b$, если она пересекает их в двух точках.
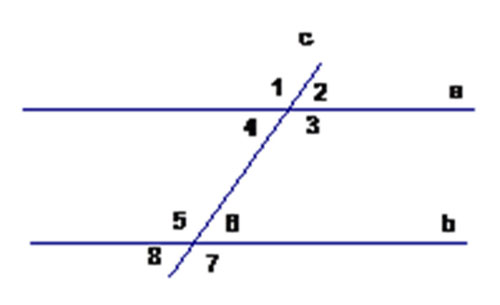
Рассмотрим две прямые $a$ и $b$ и секущую прямую $с$.
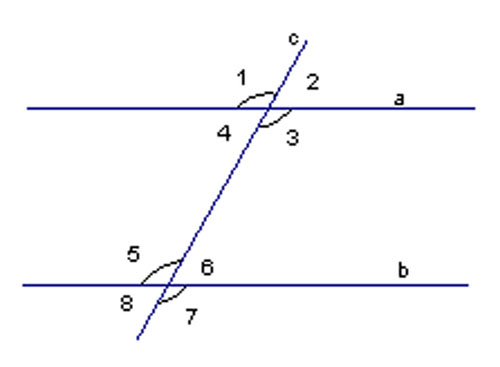
При их пересечении возникают углы, которые обозначим цифрами от $1$ до $8$.
У каждого из этих углов есть название, которое часто приходиться употреблять в математике:
- пары углов $3$ и $5$, $4$ и $6$ называются накрест лежащими;
- пары углов $1$ и $5$, $4$ и $8$, $2$ и $6$, $3$ и $7$ называют соответственными;
- пары углов $4$ и $5$, $5$ и $6$ называют односторонними.
Признаки параллельности прямых
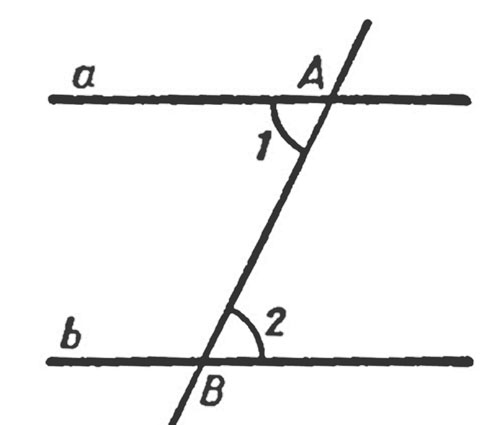
Равенство пары накрест лежащих углов для прямых $a$ и $b$ и секущей $с$ говорит о том, что прямые $a$ и $b$ – параллельны:
если $∠1=∠2$, то $a \parallel b$.
Доказательство.
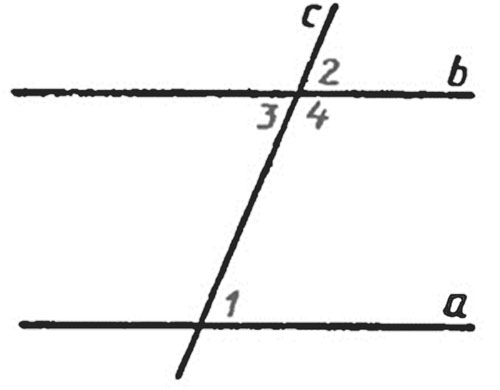
Пусть накрест лежащие углы для прямых $а$ и $b$ и секущей $с$ равны: $∠1=∠2$.
Покажем, что $a \parallel b$.
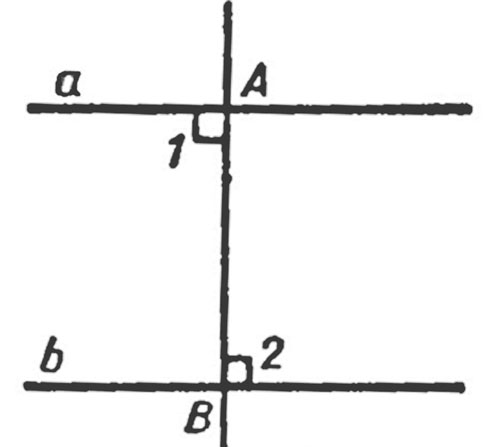
При условии, что углы $1$ и $2$ будут прямыми, получим, что прямые $а$ и $b$ будут перпендикулярными относительно прямой $АВ$, а значит – параллельными.
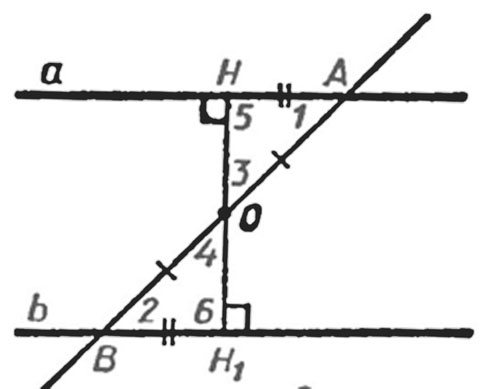
При условии, что углы $1$ и $2$ не являются прямыми, проведем из точки $О$ – середины отрезка $АВ$, перпендикуляр $ОН$ к прямой $а$.
На прямой $b$ отложим отрезок $BH_1=AH$ и проведем отрезок $OH_1$. Получаем два равных треугольника $ОНА$ и $ОH_1В$ по двум сторонам и углу между ними ($∠1=∠2$, $АО=ВО$, $BH_1=AH$), поэтому $∠3=∠4$ и $∠5=∠6$. Т.к. $∠3=∠4$, то точка $H_1$ лежит на луче $ОН$, таким образом точки $Н$, $О$ и $H_1$ принадлежат одной прямой. Т.к. $∠5=∠6$, то $∠6=90^{\circ}$. Таким образом, прямые $а$ и $b$ являются перпендикулярными относительно прямой $HH_1$ являются параллельными. Теорема доказана.
Равенство пары соответственных углов для прямых $a$ и $b$ и секущей $с$ говорит о том, что прямые $a$ и $b$ – параллельны:
если $∠1=∠2$, то $a \parallel b$.
Доказательство.
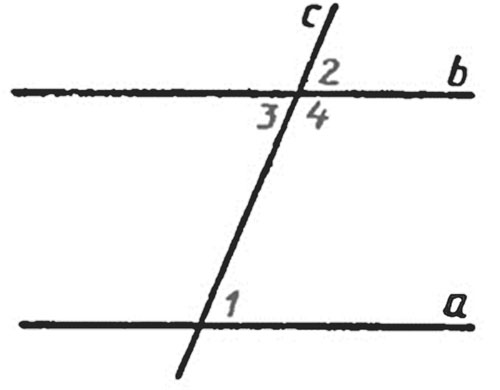
Пусть соответственные углы для прямых $а$ и $b$ и секущей $с$ равны: $∠1=∠2$. Углы $2$ и $3$ являются вертикальными, поэтому $∠2=∠3$. Значит $∠1=∠3$. Т.к. углы $1$ и $3$ – накрест лежащие, то прямые $а$ и $b$ являются параллельными. Теорема доказана.
Если сумма двух односторонних углов для прямых $a$ и $b$ и секущей $с$ равна $180^{\circ}C$, то прямые $a$ и $b$ – параллельны:
если $∠1+∠4=180^{\circ}$, то $a \parallel b$.
Доказательство.
Пусть односторонние углы для прямых $а$ и $b$ и секущей $с$ в сумме дают $180^{\circ}$, например
$∠1+∠4=180^{\circ}$.
Углы $3$ и $4$ являются смежными, поэтому
$∠3+∠4=180^{\circ}$.
Из полученных равенств видно, что накрест лежащие углы $∠1=∠3$, из чего следует, что прямые $а$ и $b$ являются параллельными.
Теорема доказана.
Из рассмотренных признаков вытекает параллельность прямых.
Примеры решения задач
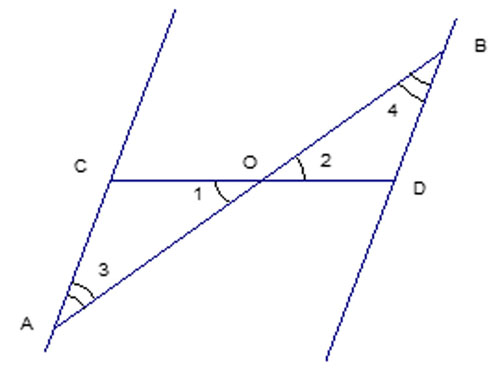
Точка пересечения делит отрезки $АВ$ и $CD$ пополам. Доказать, что $AC \parallel BD$.
Дано: $AO=OB$, $CO=OD$.
Доказать: $AC \parallel BD$.
Доказательство.
Из условия задачи $AO=OB$, $CO=OD$ и равенства вертикальных углов $∠1=∠2$ согласно I-му признаку равенства треугольников следует, что $\bigtriangleup COA=\bigtriangleup DOB$. Таким образом, $∠3=∠4$.
Углы $3$ и $4$ – накрест лежащие при двух прямых $AC$ и $BD$ и секущей $AB$. Тогда согласно I-му признаку параллельности прямых $AC \parallel BD$. Утверждение доказано.
Дан угол $∠2=45^{\circ}$, а $∠7$ в $3$ раза больше данного угла. Доказать, что $a \parallel b$.
Дано: $∠2=45^{\circ}$, $∠7=3∠2$.
Доказать: $a \parallel b$.
Доказательство:
- Найдем значение угла $7$:
$∠7=3 \cdot 45^{\circ}=135^{\circ}$.
- Вертикальные углы $∠5=∠7=135^{\circ}$, $∠2=∠4=45^{\circ}$.
- Найдем сумму внутренних углов $∠5+∠4=135^{\circ}+45^{\circ}=180^{\circ}$.
Согласно III-му признаку параллельности прямых $a \parallel b$. Утверждение доказано.
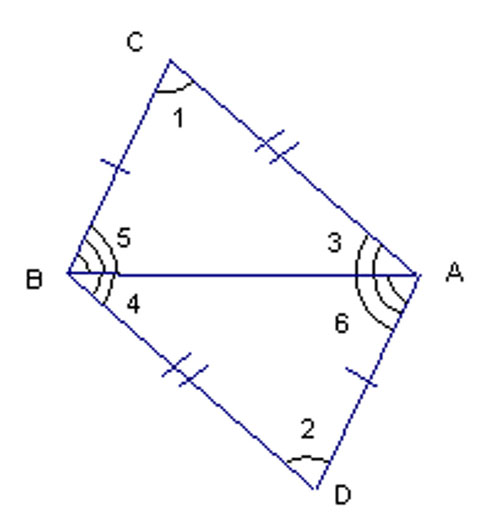
Дано: $\bigtriangleup ABC=\bigtriangleup ADB$.
Доказать: $AC \parallel BD$, $AD \parallel BC$.
Доказательство:
У рассматриваемых рисунков сторона $АВ$ – общая.
Т.к. треугольники $АВС$ и $ADB$ равны, то $AD=CB$, $AC=BD$, а также соответствующие углы равны $∠1=∠2$, $∠3=∠4$, $∠5=∠6$.
Пара углов $3$ и $4$ – накрест лежащие для прямых $АС$ и $BD$ и соответствующей секущей $АВ$, поэтому согласно I-му признаку параллельности прямых $AC \parallel BD$.
Пара углов $5$ и $6$ – накрест лежащие для прямых $AD$ и $BC$ и соответствующей секущей $АВ$, поэтому согласно I-му признаку параллельности прямых $AD \parallel BC$.