Типы зависимостей
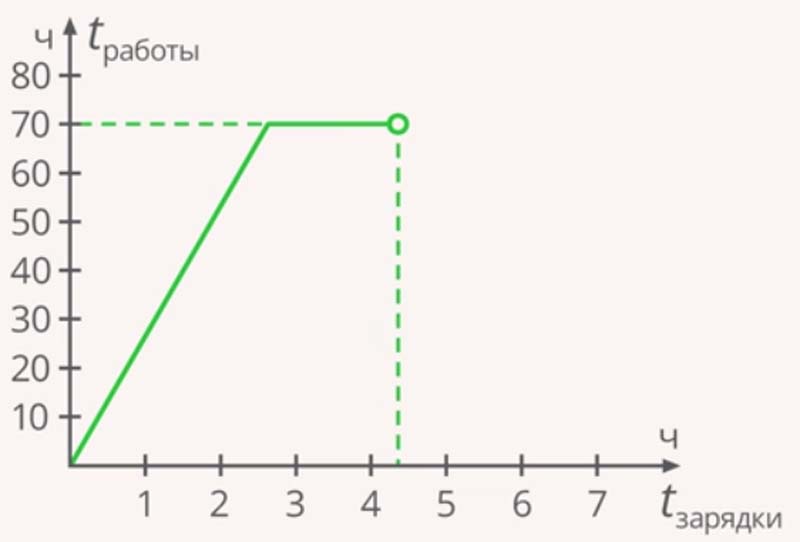
Рассмотрим зарядку батареи. В качестве первой величины возьмем время, которое она заряжается. Вторая величина – время, которое она будет работать после зарядки. Чем дольше будет заряжаться батарея, тем дольше она будет работать. Процесс будет длиться до тех пор, пока батарея не полностью зарядится.
Зависимость времени работы батареи от времени, которое она заряжается
Такая зависимость называется прямой:
С увеличением одной величины увеличивается и вторая. С уменьшением одной величины уменьшается и вторая величина.
Рассмотрим другой пример.
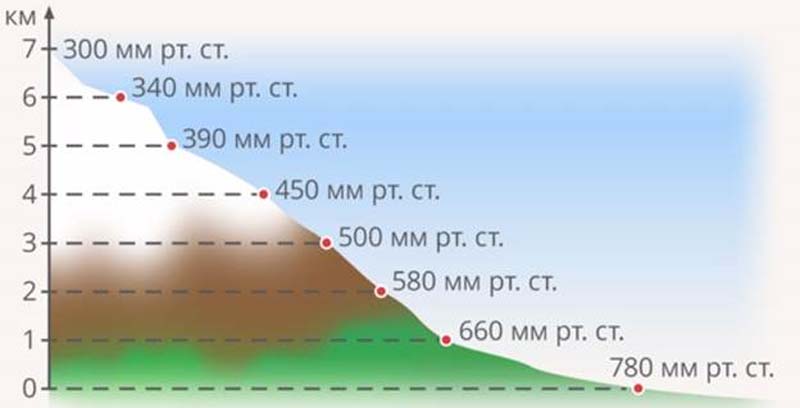
Чем больше книг прочитает ученик, тем меньше ошибок сделает в диктанте. Или чем выше подняться в горы, тем ниже будет атмосферное давление.
Такая зависимость называется обратной:
С увеличением одной величины уменьшается вторая. С уменьшением одной величины увеличивается вторая величина.
Таким образом, в случае прямой зависимости обе величины изменяются одинаково (обе либо увеличиваются, либо уменьшаются), а в случае обратной зависимости – противоположно (одна увеличивается, а другая уменьшается либо наоборот).
Определение зависимостей между величинами
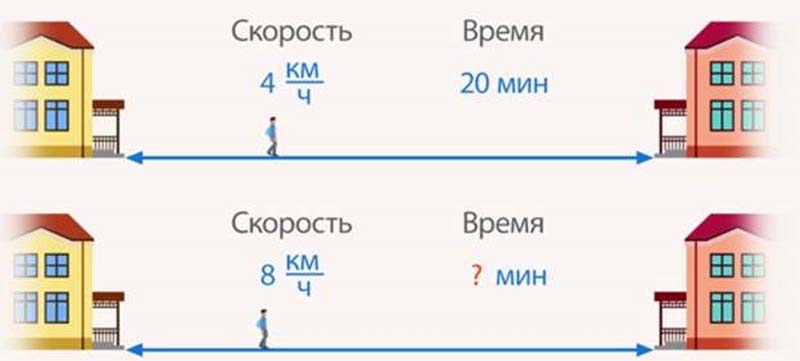
Время, затраченное для похода в гости к другу, составляет $20$ минут. При увеличении скорости (первой величины) в $2$ раза найдем, как изменится время (вторая величина), которое будет затрачено на путь к другу.
Очевидно, что время уменьшится в $2$ раза.
Такую зависимость называют пропорциональной:
Во сколько раз изменится одна величина, во столько раз изменится и вторая.
За $2$ булки хлеба в магазине нужно заплатить 80 рублей. Если нужно купить $4$ булки хлеба (количество хлеба увеличивается в $2$ раза), во сколько раз придется больше заплатить?
Очевидно, что стоимость также увеличится в $2$ раза. Имеем пример пропорциональной зависимости.
В обоих примерах были рассмотрены пропорциональные зависимости. Но в примере с булками хлеба величины изменяются в одну сторону, следовательно, зависимость является прямой. А в примере с походом к другу зависимость между скоростью и временем – обратная. Таким образом, существует прямо пропорциональная зависимость и обратно пропорциональная зависимость.
Прямая пропорциональность
Рассмотрим $2$ пропорциональные величины: количество булок хлеба и их стоимость. Пусть $2$ булки хлеба стоят $80$ рублей. При увеличении количества булок в $4$ раза ($8$ булок) их общая стоимость будет составлять $320$ рублей.
Отношение количества булок: $\frac{8}{2}=4$.
Отношение стоимости булок: $\frac{320}{80}=4$.
Как видно, эти отношения равны между собой:
$\frac{8}{2}=\frac{320}{80}$.
Равенство двух отношений называется пропорцией.
При прямо пропорциональной зависимости получается отношение, когда изменение первой и второй величины совпадает:
$\frac{A_2}{A_1}=\frac{B_2}{B_1}$.
Две величины называются прямо пропорциональными, если при изменении (увеличении или уменьшении) одной из них во столько же раз изменяется (увеличивается или уменьшается соответственно) и другая величина.
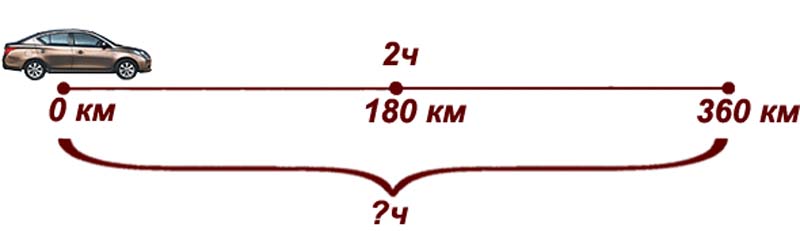
Автомобиль проехал $180$ км за $2$ часа. Найти время, за которое он с той же скоростью проедет в $2$ раза большее расстояние.
Решение.
Время прямо пропорционально расстоянию:
$t=\frac{S}{v}$.
Во сколько раз увеличится расстояние, при постоянной скорости, во столько же раз увеличится время:
$\frac{2S}{v}=2t$;
$\frac{3S}{v}=3t$.
Запишем условие задачи в виде таблицы:
Автомобиль проехал $180$ км – за время $2$ часа
Автомобиль проедет $180 \cdot 2=360$ км – за время $x$ часов
Чем больше расстояние проедет автомобиль, тем большее время ему понадобится. Следовательно, зависимость между величинами прямо пропорциональная.
Составим пропорцию:
$\frac{180}{360}=\frac{2}{x}$;
$x=\frac{360 \cdot 2}{180}$;
$x=4$.
Ответ: автомобилю потребуется $4$ часа.
Обратная пропорциональность
При обратно пропорциональной зависимости получается отношение, первая часть которого показывает, во сколько раз увеличилась первая величина, а вторая часть – во сколько раз уменьшилась вторая:
$\frac{N_2}{N_1}=\frac{S_1}{S_2}$.
Две величины называются обратно пропорциональными, если при изменении (увеличении или уменьшении) одной из них во столько же раз изменится (уменьшится или увеличится соответственно) другая величина.
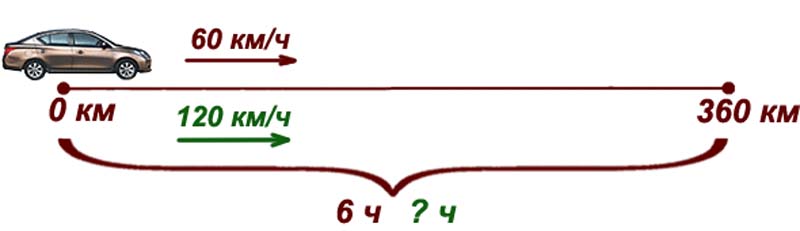
Автомобиль, который двигается со скоростью $60$ км/ч, проехал путь за $6$ часов. Найти время, за которое автомобиль проедет этот же путь, но со скоростью в $2$ раза больше прежней.
Решение.
Время обратно пропорционально скорости:
$t=\frac{S}{v}$.
Во сколько раз увеличивается скорость, при том же пути, во столько же раз уменьшается время:
$\frac{S}{2v}=\frac{t}{2}$;
$\frac{S}{3v}=\frac{t}{3}$.
Запишем условие задачи в виде таблицы:
Автомобиль проехал $60$ км - за время $6$ часов
Автомобиль проедет $120$ км – за время $x$ часов
Чем больше скорость автомобиля, тем меньше времени ему понадобится. Следовательно, зависимость между величинами обратно пропорциональная.
Составим пропорцию.
Т.к. пропорциональность обратная, второе отношение в пропорции переворачиваем:
$\frac{60}{120}=\frac{x}{6}$;
$x=\frac{60 \cdot 6}{120}$;
$x=3$.
Ответ: автомобилю потребуется $3$ часа.