Сложение натуральных чисел
Для получения числа, которое следует за натуральным, нужно прибавить к нему единицу.
$5 + 1 = 6;$
$48 + 1 = 49$
Для сложения чисел $9$ и $3$ нужно к числу $9$ прибавить $3$ раза единицу.
Получим:
$9 + 3 = 9 + 1 + 1 + 1 = 10 + 1 +1 = 11 + 1 = 12.$
Записывают короче:
$9 + 3 = 12.$
Числа, которые складывают, называют слагаемыми, а результат их сложения -- суммой.
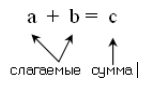
Рисунок 1.
В примере $9 + 3 = 12$:
$9$ и $3$ -- слагаемые, $6$ -- сумма.
Свойства сложения
-
Переместительное свойство (коммутативность):
При перестановке слагаемых сумма не меняется
$1 + 5 = 5 + 1 = 6.$
В общем виде переместительное свойство записывается так:
$a + b = b + a$.
-
Сочетательное свойство (ассоциативность):
Сумма трех и более слагаемых не изменится, если изменить порядок их сложения
$2 + ( 8 + 3 ) = ( 2 + 8 ) + 3 = 13.$
В общем виде сочетательное свойство записывается так:
$a + ( b + c ) = ( a + b ) + c.$
-
Свойство прибавления нуля:
Если к числу прибавить нуль, то сумма будет равна самому числу
$7 + 0 = 7.$
К этому свойству можно применить переместительное свойство, получим:
Если к нулю прибавить число, то сумма будет равна прибавляемому числу
$0 + 7 = 7.$
В общем виде:
$a + 0 = 0 + a = a.$
Если точкой $C$ разделить отрезок $AB$, то сумма длин отрезков $AC$ и $CB$ будет равна длине отрезка $AB$.

Рисунок 2.Записывается: $AB = AC + CB$.
Сложение чисел можно удобно выполнять «в столбик»:

Рисунок 3.
Вычитание натуральных чисел
Вычитание -- операция, обратная сложению.
На тарелке лежало $7$ яблок, съели $3$ яблока. Сколько яблок осталось на тарелке?
Очевидно, что если к оставшемуся числу яблок $(x)$ добавить $3$ яблока, то их станет $7$:
$x + 3 = 7.$
Таким образом, известно одно слагаемое и сумма, нужно найти второе слагаемое.
Для этого используется вычитание:
$x = 7 - 3 = 4$, т.к. $3 + 4 = 7.$
Число, из которого вычитают, называется уменьшаемым, а число, которое вычитают, -- вычитаемым. Результат вычитания называется разностью.
Из данной задачи получаем:
$7$ -- уменьшаемое, $3$ -- вычитаемое, $8$ -- разность.
В общем виде
Если $b + c = a$, то
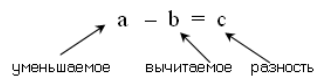
Рисунок 4.
При вычитании натуральных чисел уменьшаемое обязательно должно быть больше вычитаемого:
$11 - 3 = 8; 8 > 3.$
Разность двух чисел находят, чтобы узнать на сколько уменьшаемое больше вычитаемого или на сколько вычитаемое меньше уменьшаемого:
$11$ больше $3$ на $8$.
Свойства вычитания
-
Свойство вычитания суммы из числа:
$a - ( b + c ) = a - b - c.$
Например, нужно найти значение выражения:
$123 - ( 23 + 45 ) = 123 - 68 = 55.$
Однако намного удобнее считать так:
$123 - ( 23 + 45 ) = 123 - 23 - 45 = 100 - 45 = 55.$
В этом выражении нужно вычесть сумму из числа, а можно сначала вычесть из уменьшаемого одно слагаемое, а потом из полученной разности вычесть второе слагаемое.
Например, найдем результат выражения:
$217 - 33 - 27 = 184 - 27 = 157.$
Но гораздо легче найти сумму вычитаемых и вычесть ее из уменьшаемого:
$217 - 33 - 23 = 217 - ( 33 + 27 ) = 217 - 60 = 157.$
-
Свойство вычитания числа из суммы:
если $c
если $c
Рассмотрим три примера с одинаковыми результатами.
$( 6 + 5 ) - 4=11 - 4=7;$
$6 + ( 5 - 4 )=6 + 1=7;$
$( 6 - 4 ) + 5=2 + 5=7.$
Откуда получаем: $( 6 + 5 ) - 4=6 + ( 5 - 4 )=( 6 - 4 ) + 5.$
Если нужно вычесть число из суммы, можно вычесть его из любого слагаемого и к полученной разности прибавить другое слагаемое.
Вычитаемое обязательно должно быть меньше слагаемого, из которого его вычитают, или равным ему.
Пример 3$( 234 + 123 ) - 134=357 - 134=223.$
Но намного удобнее считать так:
$( 234 + 123 ) - 134=234 - 134+ 123=100+ 123=223.$
-
Если из числа вычесть нуль, оно не изменится:
$a - 0 = a.$
Если из числа вычесть это же число, получим нуль:
$a - a = 0.$
Т.к. $9 + 0 = 9$, то по смыслу вычитания имеем:
$9 - 9 = 0$ или $9 - 0 = 9.$
Результат вычитания удобно находить «в столбик»:
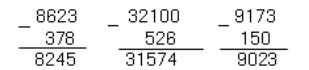
Рисунок 5.Если точкой $C$ разделяется отрезок $AB$, то разность длин отрезков $AB$ и CB$ равна длине отрезка $AC.$

Рисунок 6.Записывается: $AB - CB = AC$ или $AB - AC = CB.$
Если $AB = 7$ см, а $CB = 4$ см, то $AC = 7 - 4 = 3$ см.
Пример 4Решить уравнение $63 - x = 55.$
Решение:
$x = 63 - 55$, откуда $x = 8.$
Число $8$ называется корнем уравнения $63 - x = 55$, т.к. получаем верное равенство $63 - 8 = 55.$
Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность.











