Понятие параллелепипеда
Геометрическая фигура, образованная двумя равными параллелограммами, лежащими в параллельных плоскостях, а их вершины соединены между собой так, что между параллельными плоскостями образуются две пары параллелограммов, лежащих в параллельных плоскостях, называется параллелепипедом (рис. 1).
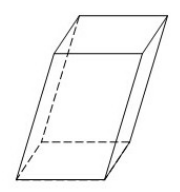
Рисунок 1. Параллелепипед
Параллелограммы, из которых составлен параллелепипед, называются гранями параллелепипеда, стороны параллелограммов -- сторонами параллелепипеда, а вершины параллелограммов -- вершинами параллелепипеда.
Свойства параллелепипеда
Противоположные грани параллелепипеда равны между собой и параллельны.
Доказательство.
Параллельность противоположных граней сразу исходит из определения 1.
Докажем равенство противоположных граней. Для этого рассмотрим рисунок 2.
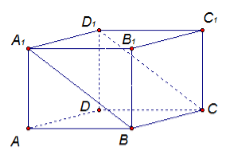
Рисунок 2.
Рассмотрим грани ${AA}_1B_1B$ и ${DD}_1C_1C$. Так как, по определению 1, грани параллелепипеда -- параллелограммы, то ${AA}_1={DD}_1$ и $AB=DC.$ Так же ${AA}_1||{DD}_1$ и $AB||DC$, следовательно, $\overrightarrow{{AA}_1}\uparrow \uparrow \overrightarrow{{DD}_1}$ и $\overrightarrow{AB}\uparrow \uparrow \overrightarrow{DC}$, то есть $\angle A_1AB=\angle D_1DC$. Значит, по I признаку равенства треугольников$\triangle A_1AB=\triangle D_1DC$. Аналогично доказывается, что $\triangle D_1C_1C=\triangle A_1B_1B$, следовательно, $D_1C_1CD=A_1B_1BA$. Аналогично доказывается равенство других противоположных граней.
Теорема доказана.
Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.
Доказательство.
Рассмотрим рисунок 3.
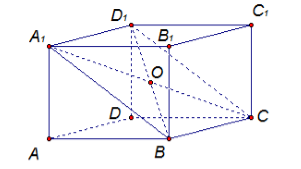
Рисунок 3.
Докажем вначале, что диагонали $A_1C$ и $D_1B$ делятся точкой пересечения $O$ пополам. По теореме 1, имеем $A_1D_1=BC$ и $A_1D_1||BC$. Следовательно, $A_1D_1CB$ -- параллелограмм. Тогда, по свойству параллелограмма, получим, что диагонали $A_1C$ и $D_1B$ делятся точкой пересечения $O$ пополам. Аналогично доказывается, что диагонали ${AC}_1$ и $D_1B$ и $A_1C$ и ${DB}_1$ делятся точками их пересечения пополам. Но, так как $O$ центр диагоналей $A_1C$ и $D_1B$, то все диагонали пересекаются в этой точке.
Теорема доказана.
Прямоугольный параллелепипед
Можно выделить два частных случая понятия параллелепипеда. Один из них -- понятие прямоугольного параллелепипеда.
Параллелепипед, у которого в основаниях лежат прямоугольники и все двугранные углы равны ${90}^0$ называется прямоугольным (рис. 4).
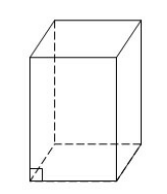Прямоугольный параллелепипед">
Рисунок 4. Прямоугольный параллелепипед
Прямоугольный параллелепипед обладает теми же свойствами, что и произвольный, однако он помимо этого обладает отдельным свойством.
Сумма квадратов трех измерений (высота, длина и ширина) равняется квадрату его диагонали.
Математически это можно записать следующим образом:
\[d^2=a^2+b^2+c^2\]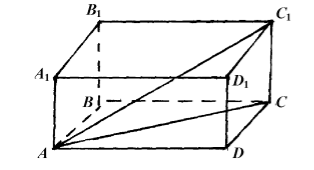
Рисунок 5.
Доказательство.
Рассмотрим рисунок 5. Докажем, для примера, что
Рассмотрим треугольник $ADC$. По теореме Пифагора, имеем
Так как $ABCD$ -- прямоугольник, то $DC=AB$, следовательно
Рассмотрим треугольник $ACC_1$. По теореме Пифагора, имеем
Так как ${CC}_1=AA_1$, то
Куб
Прямоугольный параллелепипед, гранями которого служат квадраты, называется кубом (рис. 6).
Рисунок 6.
Пример задачи
Найти длину диагонали куба, у которого высота равняется $3$.
Решение.
По определению куба, получим, что мы имеем прямоугольный параллелепипед, у которого и высота. И ширина и длина равны 3. Тогда, по теореме 3, имеем
\[d^2=3^2+3^2+3^2\] \[d^2=27\] \[d=3\sqrt{3}\]Ответ: $3\sqrt{3}$.
