Луч
Определение понятия луча базируется на двух основных понятиях геометрии: точке и прямой. Возьмем произвольную прямую и выберем на ней произвольную точку. Такая точка будет разделять эту прямую две части (рис. 1).
Лучем будет называться часть прямой, которая ограничена какой-либо точкой на этой прямой, но только с одной стороны.
Точка, которой ограничен луч в рамках определения 1 называется началом этого луча.
отметим, что угол, который получался на рисунке 1 называется развернутым.
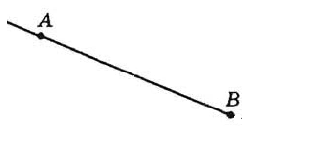
Луч будем обозначать двумя точками: началом его и другой любой произвольной точки на нем. Отметим, что здесь, в обозначении, важен порядок обозначения этих точек. На первом месте всегда ставим именно начало луча (рис. 2)
Понятие луча связано со следующей аксиомой геометрии:
Аксиома 1: Любая произвольная точка на прямой будет делить ее на два луча, причем любые произвольные точки одно и того же из них будут лежать с одной стороны от этой точки, а две точки из разных лучей – по разные стороны от этой точки.
С понятием луча и отрезка также связана следующая аксиома.
Аксиома 2: От начала любого луча может быть отложен отрезок, который равен заведомо данному отрезку, причем такой отрезок будет единственен.
Угол
Пусть нам даны два произвольных луча. Наложим их начала друг на друга. Тогда
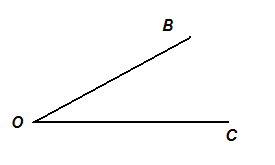
Углом будем называть два луча, которые имеют одно и тоже начало.
Точка, которая является началом лучей в рамках определения 3, называется вершиной этого угла.
Угол будем обозначать следующими тремя её точками: вершиной, точкой на одном из лучей и точкой на другом луче, причем вершина угла записывается в середине его обозначения (рис. 3).
С понятием луча и угла также связана следующая аксиома.
Аксиома 3: От любого произвольного луча может быть отложен угол в определенную полуплоскость, который равен заведомо данному углу, причем такой угол будет единственен.
Сравнение углов
Рассмотрим два произвольных угла. Очевидно, что они могут быть либо равными, либо неравными.
Итак, для сравнения выбранных нами углов (обозначим их угол 1 и угол 2) наложим вершину угла 1 на вершину угла 2, так, чтобы, по одному из лучей этих углов наложились друг на друга, а другие два были по одну сторону от этих лучей. После такого наложения возможны два следующих случая:
-
Вторые лучи этих углов также совпадут. В таком случае мы получим, что такие углы будут равны друг другу (рис. 4).
-
Вторые лучи не совпадут. Здесь, без ограничения общности, будем считать, что луч угла 1 будет лежать внутри угла 2. Тогда здесь мы говорим, что данные углы не равны, причем угол 1 меньше угла 2 (рис. 5).
Величина угла
Помимо сравнения одних углов с другими также часто необходимо измерение углов. Измерить угол означает найти его величину. Для этого необходимо выбрать какой-то «эталонный» угол, который мы будем принимать за единицу. Чаще всего таким углом является угол, который равен $\frac{1}{180}$ части развернутого угла. Такую величину называют градусом. После выбора такого угла мы проводим с ним сравнение углов, величину которого нужно найти.
Самым простым способом измерения величины углов является измерение с помощью транспортира.
Найти величину следующего угла:
Решение.
Используем транспортир:
Получим
Ответ: $30^0$.
После определения величины углов у нас появляется второй способ для сравнения углов. Если при одном и том же выборе единицы измерения угол 1 и угол 2 будут иметь одинаковую величину, то такие углы будут называться равными. Если же, без ограничения общности, угол 1 будет иметь величину по числовому значению меньше величины угла 2, то угол 1 будет меньше угла 2.
Виды углов
Угол называется острым, если он меньше $90^0$.
Угол называется тупым, если он больше $90^0$.
Угол называется развернутым, если он равен $180^0$.
Угол называется прямым, если он равен $90^0$.
Определить виды следующих углов:
Решение.
Из определений 5-8, получим.
Ответ:
- тупой.
- развернутый.
- прямой.
- острый.