В этой статье мы приведем начальные сведение об основных понятиях геометрии, а именно о прямой, луче, отрезке и угле.
Прямая
Возьмем линейку и, не отрывая карандаша, проведем линию произвольной длины. Полученную линию мы и будем называть прямой. Однако тут необходимо отметить, что это не вся прямая, а только её часть. Всю же прямую построить не имеется возможным, она является бесконечной на обоих своих концах.
Прямые будем обозначать маленькой латинской буквой, либо двумя её точками в круглых скобках (рис. 1).
Для двух прямых актуально их взаимное расположение. Возможны три случая:
- Две прямые совпадают. В этом случае каждая точка одной будет также и точкой другой прямой.
- Две прямые пересекаются. В этом случае только какая-то одна точка из одной прямой будет также принадлежать и другой прямой.
- Две прямые параллельны. В этом случае у каждой из этих прямых свой набор различных друг от друга точек.
В рамках второго случая отдельно выделяются перпендикулярные прямые.
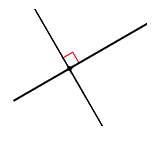
Рассмотрим две произвольные пересекающиеся прямые. Очевидно, что в точке их пересечения образовывается $4$ угла. Тогда
Пересекающиеся прямые будем называть перпендикулярными, если хотя бы один угол, образованный их пересечением равняется $90^0$ (рис. 2).
Обозначение: $a⊥b$
Перпендикулярные прямые связаны со следующей теоремой
Две прямые, являющиеся перпендикулярными для третьей будут непересекающимися.
Луч
Возьмем произвольную прямую и выберем на ней произвольную точку. Такая точка будет разделять эту прямую две части. Тогда:
Лучем будет называться часть прямой, которая ограничена какой-либо точкой на этой прямой, но только с одной стороны.
Точка, которой ограничен луч в рамках определения 1, называется началом этого луча.
Луч будем обозначать двумя точками: началом его и другой любой произвольной точки на нем. Отметим, что здесь, в обозначении, важен порядок обозначения этих точек. На первом месте всегда ставим именно начало луча (рис.3)
Отрезок
Пусть нам дана произвольная прямая и две точки, принадлежащие ей. Тогда:
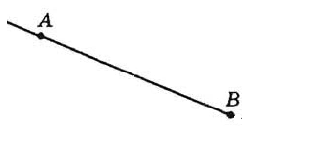
Отрезком будет называться часть прямой, которая ограничена двумя ее произвольными различными точками.
Точки, которыми ограничен отрезок в рамках определения 1, называются концами этого отрезка.
Отрезки будем обозначать двумя её точками концов в квадратных скобках (рис. 4).
![Отрезок [AB]](/assets/files/articles/math806.png)
Для отрезков важно такое понятие, как их измерение. Измерить отрезок означает найти его длину. Для этого необходимо выбрать какой-то «эталонный» отрезок, который мы будем принимать за единицу ( к примеру отрезок, длина которого равняется $1$ сантиметру). После выбора такого отрезка мы проводим с ним сравнение отрезков, длину которого нужно найти.
Самым простым способом измерения длины отрезков является измерение, с помощью линейки.
Угол
Пусть нам даны два произвольных луча. Наложим их начала друг на друга. Тогда:
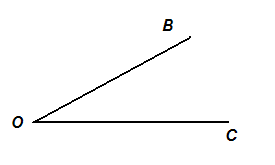
Углом будем называть два луча, которые имеют одно и тоже начало.
Точка, которая является началом лучей в рамках определения 3, называется вершиной этого угла.
Угол будем обозначать следующими тремя её точками: вершиной, точкой на одном из лучей и точкой на другом луче, причем вершина угла записывается в середине его обозначения (рис. 5).
На практике часто необходимо измерение углов. Измерить угол означает найти его величину. Для этого необходимо выбрать какой-то «эталонный» угол, который мы будем принимать за единицу. Чаще всего таким углом является угол, который равен $\frac{1}{180}$ части развернутого угла. Такую величину называют градусом. После выбора такого угла мы проводим с ним сравнение углов, величину которого нужно найти.
Самым простым способом измерения величины углов является измерение с помощью транспортира.
Пример задачи
Рассмотрим пример задачи связанной с основными понятиями геометрии.
Даны две прямые, которые имеют точку пересечения. Через точку, которая не принадлежит ни одной из них проведены две прямые, одна из которых перпендикулярна одной из выше описанных прямых, а другая - другой из них. Доказать, что они не совпадают.
Решение.
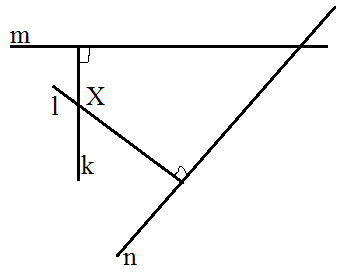
Изобразим рисунок по условию задачи.
Из условия задачи будем иметь, что $m⊥k,n⊥l$.
Предположим противное, пусть прямые $k$ и $l$ совпадают. Пусть это будет прямой $l$. Тогда, по условию $m⊥l$ и $n⊥l$. Следовательно, по теореме 1, прямые $m$ и $n$ не пересекаются. Получили противоречие, а значит прямые $k$ и $l$ не совпадают.