Выражение вида $z=a+bi$ , где $a$ и $b$ - вещественные числа, а $i$ - «мнимая единица», называется комплексным числом $z$. Мнимая единица определяется равенством $i=\sqrt {-1}$ или $i^2=-1$.
Запись некоторого комплексного числа $z$ в виде $z=r \cdot (cos \varphi + isin \varphi)$ называется тригонометрической формой записи, при этом число $r$ - модуль данного комплексного числа $z$, $\varphi$ - аргумент данного комплексного числа $z$.
Модуль некоторого комплексного числа вычисляется по следующей формуле:
$$r=|z|=|a+bi|= \ sqrt {a^2+b^2}$$Аргумент $\varphi$ некоторого комплексного числа $z=a+bi$ можно вычислить, используя следующие формулы:
$$\varphi = tg \frac {b}{a}; cos \varphi = \frac {a}{\sqrt {a^2+b^2}}; sin \varphi = \frac {b}{\sqrt {a^2+b^2}}$$На практике для вычисления значения аргумента заданного комплексного числа $z=a+bi$ обычно пользуются формулой:
$$ \varphi = arg z = \begin{equation*} \begin{cases} arctg \frac {b}{a}, a \ge 0, (*) \\ arctg \frac{b} {a} + \pi, a или решают систему уравнений $$ \begin{equation*} \begin{cases} cos \varphi = \frac {a} {\sqrt {a^2+b^2}}, (**) \\ sin \varphi = \frac {b} {\sqrt {a^2+b^2}} \end{cases} \end{equation*}$$Рассмотрим комплексное число в тригонометрической форме
$$z=r \cdot (cos \varphi + i sin \varphi)$$Используя формулу Эйлера, получим:
$$cos \varphi + i sin \varphi = e^{i \varphi}$$Подставим полученное значение в тригонометрическую запись некоторого комплексного числа и получим:
$$z=r \cdot e^{i \varphi}$$Запись комплексного числа $z$ в виде $z=r \cdot e^{i \varphi}$ называется показательной формой записи, где число $r$ - модуль комплексного числа $z$, $ \varphi$ - аргумент комплексного числа $z$.
Комплексное число, представленное в показательной форме, так же как и число в тригонометрической форме, легко изображается на комплексной плоскости с помощью аргумента и модуля заданного числа. При этом угол отсчитывается от положительного направления оси $Ox$ по/против часовой стрелки (в зависимости от знака аргумента) и от начала координат на полученном луче откладывается отрезок длины равной модулю комплексного числа (рис.1).
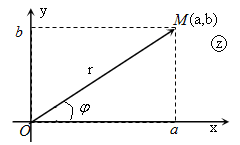
Рис. 1.
Представить в показательной форме заданные комплексные числа, для которых:
1) $r=0, \varphi = 5 \pi$; 2) $r=10, \varphi= \frac {\pi}{2}$ ; 3) $r= \sqrt{2}, \varphi =- \frac {\pi}{3}$; 4)$r=3, \varphi=0$.Решение:
Показательная форма записи некоторого комплексного числа имеет вид $z=r \cdot e^{i \varphi}$.
Для $r=0, \varphi = 5 \pi$ получаем комплексное число $z=0 \cdot e^{i \cdot 5 \pi}$.
Для $r=10, \varphi= \frac {\pi}{2}$ получаем комплексное число $z=10 \cdot e^{i (-\frac {\pi} {3})}$.
Для $r= \sqrt {2}, \varphi =- \frac {\pi}{3}$ получаем комплексное число $z=3 \cdot e^{i \cdot 0}$.
Для получаем комплексное число $z=3 \cdot e^{i \cdot 0}$ .
Чтобы комплексное число $z$, записанное в тригонометрической форме, привести к показательной форме записи, необходимо выполнить следующее:
- определить из тригонометрической записи числа значения модуля и аргумента;
- подставить полученные значения в выражение $z=r \cdot e^{i \varphi}$.
Представить заданные комплексные числа в показательной форме: 1) $z=3 \cdot (cos \frac {\pi}{3} + i sin {\pi}{3}$; 2)$z=6 \cdot (cos \pi + i sin \pi)$.
Решение:
Показательная форма записи некоторого комплексного числа имеет вид $z=r \cdot e^{i \varphi}$.
1) Определим значения модуля и аргумента: $r=3, \varphi = \frac {\pi}{3}$.
Запись числа в показательной форме имеет вид: $z=3 \cdot e^{\frac {\pi}{3}i}$.
2) Определим значения модуля и аргумента: $r=6; \varphi = \pi$.
Запись числа в показательной форме имеет вид: $z=6 \cdot e^{\pi \cdot i}$.
Запись некоторого комплексного числа $z$ в виде $z=a+bi$ называется алгебраической формой записи (или алгебраической записью) комплексного числа. При этом:
- $a$ - вещественная (действительная) часть, обозначение Re $z=a$;
- $b$ - мнимая часть, обозначение Im $z=b$.
Чтобы комплексное число $z$, записанное в алгебраической форме, привести к тригонометрической форме записи, необходимо выполнить следующее:
- вычислить модуль и аргумент;
- подставить полученные значения в выражение $z=r \cdot e^{i \varphi}$.
Представить заданные комплексные числа в показательной форме:
1) $z=2+0 \cdot i$; 2) $z= \frac {1}{2}+ \frac {1}{2} \cdot i$.Решение:
Показательная форма записи некоторого комплексного числа имеет вид $z=r \cdot e^{i \varphi}$.
1) По условию $a=2,b=0$.
Вычислим модуль исходного комплексного числа:
$$r= \ sqrt {2^2 + 0^2} = 2$$
Вычислим аргумент исходного комплексного числа, используя формулу (*):
$$\varphi = arg z= zrctg \frac {0}{2} = arctg0=0$$Подставим полученные значения и получим:
$$z=2 \cdot e^{i \cdot 0}$$Следовательно, $z=2 \cdot e^{i \cdot 0}$ - искомая запись комплексного числа.
2) По условию $a= \frac {1}{2},b= \frac {1}{2}$.
Вычислим модуль исходного комплексного числа:
$$r= \sqrt {\frac {1}{2}^2 + \frac {1}{2}^2} = \sqrt {\frac {1}{4}+\frac {1}{4}} = \sqrt \frac {1}{2}= \frac {\sqrt {2}}{2}$$Вычислим аргумент исходного комплексного числа, используя формулу (*):
$$\varphi = arg z=arctg \frac {1/2}{1/2} = arctgl = \frac {\pi}{4}$$Подставим полученные значения и получим:
$$z= \frac {\sqrt {2}}{2} \cdot e^{i \frac {\pi}{4}}$$Следовательно, $z= \frac {\sqrt {2}}{2} \cdot e^{i \frac {\pi}{4}}$ - искомая запись комплексного числа.
Таким образом, можно сделать вывод о том, что в каком бы виде не было записано комплексное число $z$ , его всегда можно представить в показательной форме записи $z=r \cdot e^{i \varphi}$.











