Определение функции
Существуют множество определений для понятия «функция».
Одними из классических определений понятия «функция» считаются определения на базе соответствий. Приведем ряд таких определений.
Зависимость, при которой каждому значению независимой переменной соответствует единственное значение зависимой переменной, называется функцией.
Пусть даны два непустых множества $X$ и $Y$. Соответствие $f$, которое каждому $x\in X$ сопоставляет один и только один $y\in Y$ Называется функцией ($f:X → Y$).
Пусть $M$ и $N$ - два произвольных числовых множества. Говорят, что на $M$ определена функция $f$, принимающая значения из $N$, если каждому элементу $x\in X$ поставлен в соответствие один и только один элемент из $N$.
Следующее определение дается через понятие переменной величины. Переменной величиной называется величина, которая в данном исследовании принимает различные числовые значения.
Пусть $M$ - множество значений переменной величины $x$. Тогда, сели каждому значению $x\in M$ соответствует одно определенное значение другой переменной величины $y$ есть функция величины $x$, определенной на множестве $M$.
Далее рассмотрим теоретико-множественные определения.
Пусть $X$ и $Y$ - некоторые числовые множества. Функцией называется множество $f$ упорядоченных пар чисел $(x,\ y)$ таких, что $x\in X$, $y\in Y$ и каждое $x$ входит в одну и только одну пару этого множества, а каждое $y$ входит, по крайней мере, в одну пару [15].
Всякое множество $f=\{\left(x,\ y\right)\}$ упорядоченных пар $\left(x,\ y\right)$ таких, что для любых пар $\left(x',\ y'\right)\in f$ и $\left(x'',\ y''\right)\in f$ из условия $y'≠ y''$ следует, что $x'≠x''$ называется функцией или отображением [7].
Функция $f:X → Y$ - это множество $f$ упорядоченных пар $\left(x,\ y\right)\in X\times Y$, таких, что для любого элемента $x\in X$ существует единственный элемент $y\in Y$ такой, что $\left(x,\ y\right)\in f$, то есть функция -- кортеж объектов $\left(f,\ X,\ Y\right)$.
В этих определениях
$x$ - независимая переменная.
$y$ - зависимая переменная.
Все возможные значения переменной $x$ называется областью определения функции, а все возможные значения переменной $y$ называется областью значения функции.
Далее будем рассматривать три способа для задания функций: аналитический, табличный и графический.
Аналитический способ задания функции
Для этого способа нам понадобится понятие аналитического выражения.
Аналитическим выражением называется произведение всех возможных математических операций над какими-либо числами и переменными.
Аналитическим способом задания функции и является её задание с помощью аналитического выражения.
$y=x^2+7x-3$, $y=\frac{x+5}{x+2}$, $y=cos5x$.
Приведем далее преимущества и недостатки данного способа:
Плюсы:
- С помощью формул мы можем определить значение функции для любого определенного значения переменной $x$;
- Функции, заданные таким способом можно изучать с помощью аппарата математического анализа.
Минусы:
- Малая наглядность.
- Иногда приходится производить очень громоздкие вычисления.
Табличный способ задания функции
Данный способ задания состоит в том, что для нескольких значений независимой переменной выписываются значения зависимой переменной. Все это вносится в таблицу.

Рисунок 1.
Плюс: Для любого значения независимой переменной $x$, которая внесена в таблицу, сразу узнается соответствующее значение функции $y$.
Минусы:
- Чаще всего, нет полного задания функции;
- Малая наглядность.
Графический способ задания функции
Введем понятие графика функции:
Графиком функции $f(x)$ называется множество точек координатной плоскости, которые имеют вид $(x,\ f\left(x\right))$.
Задание графика с помощью такого изображения его в декартовой системе координат называется графическим способом.
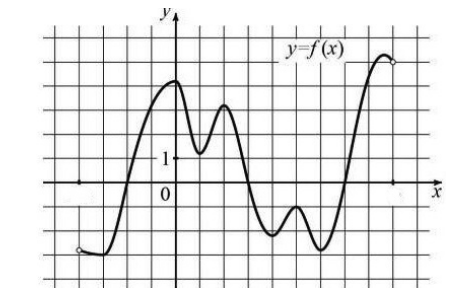
Рисунок 2.
Пример задачи
Дан аналитический вид функции $y=x^2$. Привести табличный и графический способы задания этой же функции.
Решение.
Сначала приведем табличный способ. Так как при возведении в четную степень любого числа получим неотрицательное значение, то получим следующую таблицу:

Рисунок 3.
Это и есть табличное задание.
Перейдем теперь к заданию в виде графика. Для этого отметим в декартовой системе координат точки из таблицы выше. Получим:
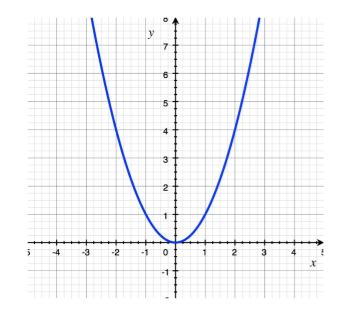
Рисунок 4.











