Формула куба разности является одной из формул сокращенного умножения. В основном, такие формулы основаны на таком понятии как Бином Ньютона. Поэтому сначала познакомимся с ним.
Бином Ньютона
Интересующая нас формула, как и многие другие, находятся с помощью формулы Бинома Ньютона.
Она будет иметь следующий вид:
$(α+β)^z=C_z^0 α^z+C_z^1 α^{z-1} β+C_z^2 α^{z-2} β^2+⋯+C_z^{z-1} αβ^{z-1}+C_z^z β^z$
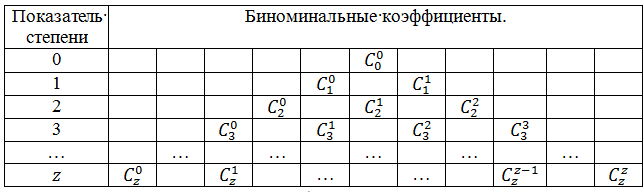
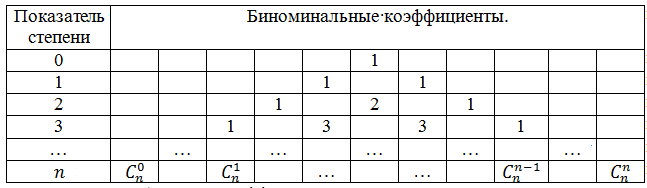
Здесь числа $C_z^0,C_z^1,…,C_z^{z-1},C_z^z$ называются коэффициентами Бинома Ньютона. Чаще всего эти коэффициенты находятся с помощью треугольника Паскаля (Таблица 1).
Вычисленные коэффициентов треугольника паскаля вы можете увидеть в таблице 2.
Формула куба разности через Бином Ньютона
Теперь, используя формулу Бинома Ньютона рассмотренную выше, мы можем вывести формулу куба разности $(α-β)^3$, учитывая, что
$(α-β)^3=(α+(-β))^3$ Из этой формулы получаем:
$(α-β)^3=C_3^0 α^3+C_3^1 α^2 (-β)+C_3^2 a(-β)^2+C_3^3 (-β)^3$
Из таблицы 2, получаем:
$C_3^0 α^3+C_3^1 α^2 (-β)+C_3^2 a(-β)^2+C_3^3 (-β)^3=α^3-3α^2 β+3aβ^2-β^3$
Следовательно, получаем что, куб разности двух выражений равняется разности кубов этих выражений, сложенным с произведением квадрата второго с первым, умноженного на три и с вычетом произведения квадрата первого со вторым, также умноженного на три, то есть:
$(α-β)^3=α^3-3α^2 β+3aβ^2-β^3$
Формула куба суммы через другие формулы
Помимо нахождения описанным выше способ, формулу куба разности можно также найти с помощью другой формулы сокращенного умножения, а именно квадрата разности:
$(α-β)^2=α^2-2aβ+β^2$
Итак, получаем:
$(α-β)^3=(α-β)^2 (α-β)=(α^2-2aβ+β^2 )(α-β)$
Далее, перемножая последние скобки, будем иметь:
$(α^2-2aβ+β^2 )(α-β)=α^3-α^2 β-2α^2 β+2aβ^2+aβ^2-β^3=α^3-3α^2 β+3aβ^2-β^3$
Следовательно, получаем что, куб разности двух выражений равняется разности кубов этих выражений, сложенным с произведением квадрата второго с первым, умноженного на три и с вычетом произведения квадрата первого со вторым, также умноженного на три, то есть:
$(α-β)^3=α^3-3α^2 β+3aβ^2-β^3$
Примеры задач
Найти куб выражения $(2x-3y)$
Решения
Из формулы куба разности, получаем:
$(2x-3y)^3=(2x)^3-3\cdot (2x)^2\cdot 3y+3\cdot 2x\cdot (3y)^2-(3y)^3=8x^3-36x^2 y+54xy^2-27y^3$
Возвести в куб:
а) $(-8α+5β)^3$
б) $(q^2+7)^3$
Решение.
а) $(-8α+5β)^3$
Так как у нас нечетная степень, то мы можем вынести знак «минус» за скобки, получим:
$(-8α+5β)^2=-(8α-5β)^3$
Используем формулу куба суммы:
$(8α-5β)^3=(8α)^3-3\cdot (8α)^2\cdot 5β+3\cdot 8α\cdot (5β)^2-(5β)^3=512α^3-960α^2 β+600αβ^2-125β^3$
Окончательно
$(-8α+5β)^3=125β^3-512α^3+960α^2 β-600αβ^2$
б) $(q^2-7)^2$
Используем формулу куба суммы:
$(q^2-7)^2=(q^2)^3-3\cdot (q^2)^2\cdot 7+3\cdot q^2\cdot 7^2-7^3=q^6-21q^4+147q^2-343$
Представить в виде куба $8x^3-12x^2+6x-1$
Решение.
Это выражение можно записать следующим образом:
$8x^3-12x^2+6x-1=(2x)^3-3\cdot (2x)^2\cdot 1+3\cdot 2x\cdot 1-1^3$
Следовательно, по формуле куба суммы
$8x^3-12x^2+6x-1=(2x-1)^3$
Вывести формулу куба разности трех выражений.
Решение.
По условию задачи нам нужно раскрыть скобки в следующем выражении
$(α-β-γ)^3$
Считая $(α-β)$ за первый член суммы, а γ за второй, по формуле куба имеем
$(α-β-γ)^3=(α-β)^3-3(α-β)^2 γ+3(α-β) γ^2-γ^3$
По формулам куба и квадрата разности, подставляя и раскрывая скобки, будем получать
$(α+β+γ)^3=α^3-3α^2 β+3aβ^2-β^3-3α^2 γ+6αβγ-3β^2 γ+3αγ^2-3βγ^2-γ^3$
Окончательно
$(α-β-γ)^3=α^3-β^3-γ^3-3α^2 β-3α^2 γ-3β^2 γ-3βγ^2+3aβ^2+3αγ^2+6αβγ$
Таким образом, используя различные такие формулы можно вывести еще множество формул для сокращенного умножения и рационального преобразования выражений. В частности они помогают и при решений конкретных математический уравнений и задач.