Определение обыкновенной дроби
Обыкновенные дроби используют для описания числа долей. Рассмотрим пример, с помощью которого можно дать определение обыкновенной дроби.
Яблоко разделили на $8$ долей. В этом случае каждая доля представляет одну восьмую долю целого яблока, т. е. $\frac{1}{8}$. Две доли обозначаются $\frac{2}{8}$, три доли -- $\frac{3}{8}$ и т.д., а $8$ долей -- $\frac{8}{8}$. Каждая из представленных записей называется обыкновенной дробью.
Приведем общее определение обыкновенной дроби.
Обыкновенной дробью называется запись вида $\frac{m}{n}$, где $m$ и $n$-- любые натуральные числа.
Часто можно встретить следующую запись обыкновенной дроби: $m/n$.
Примеры обыкновенных дробей:
\[{3}/{4}, \frac{101}{345},\ \ {23}/{5}, \frac{15}{15}, {111}/{81}.\]Числа $\frac{\sqrt{2}}{3}$, $-\frac{13}{37}$, $\frac{4}{\frac{2}{7}}$, $\frac{2,4}{8,3}$ не являются обыкновенными дробями, т.к. не подходят под вышеприведенное определение.
Числитель и знаменатель
Обыкновенная дробь состоит из числителя и знаменателя.
Числителем обыкновенной дроби $\frac{m}{n}$ называется натуральное число $m$, которое показывает количество взятых равных долей из единого целого.
Знаменателем обыкновенной дроби $\frac{m}{n}$ называется натуральное число $n$, которое показывает, на сколько равных долей разделено единое целое.

Рисунок 1.
Числитель располагается над дробной чертой, а знаменатель --под дробной чертой. Например, числителем обыкновенной дроби $\frac{5}{17}$ является число $5$, а знаменателем -- число $17$. Знаменатель показывает, что предмет разделен на $17$ долей, а числитель -- что взято $5$ таких долей.
Натуральное число как дробь со знаменателем 1
Знаменателем обыкновенной дроби может быть единица. В таком случае считают, что предмет неделим, т.е. представляет собой единое целое. Числитель такой дроби показывает, сколько целых предметов взято. Обыкновенная дробь вида $\frac{m}{1}$ имеет смысл натурального числа $m$. Таким образом получаем обоснованное равенство $\frac{m}{1}=m$.
Если переписать равенство в виде $m=\frac{m}{1}$, то оно даст возможность любое натуральное число $m$ представить в виде обыкновенной дроби. Например, число $5$ можно представить в виде дроби $\frac{5}{1}$, число $123 \ 456$ -- это дробь $\frac{123\ 456}{1}$.
Таким образом, любое натуральное число $m$ можно представить в виде обыкновенной дроби со знаменателем $1$, а любую обыкновенную дробь вида $\frac{m}{1}$ можно заменить натуральным числом $m$.
Дробная черта как знак деления
Представление предмета в виде $n$ долей является делением на $n$ равных частей. После деления предмета на $n$ долей его можно разделить поровну между $n$ людьми -- каждый получит по одной доле.
Пусть имеется $m$ одинаковых предметов, разделенных на $n$ долей. Эти $m$ предметов можно поровну разделить между $n$ людьми, если раздать каждому человеку по одной доле от каждого из $m$ предметов. При этом каждый человек получит $m$ долей $\frac{1}{n}$, которые дают обыкновенную дробь $\frac{m}{n}$. Получаем, что обыкновенная дробь $\frac{m}{n}$ может применяться для обозначения деления $m$ предметов между $n$ людьми.
Связь между обыкновенными дробями и делением выражается в том, что дробную черту можно понимать как знак деления, т.е. $\frac{m}{n}=m:n$.
Обыкновенная дробь дает возможность записывать результат деления двух натуральных чисел, для которых не выполняется деление нацело.
Например, результат деления $7$ яблок на $9$ человек можно записать как $\frac{7}{9}$, т.е. каждый получит семь девятых долей яблока: $7:9=\frac{7}{9}$.
Равные и неравные обыкновенные дроби, сравнение дробей
Результатом сравнения двух обыкновенных дробей может быть или их равенство, или их не равенство. При равенстве обыкновенных дробей их называют равными, в другом случае обыкновенные дроби называют неравными.
Обыкновенные дроби $\frac{a}{b}$ и $\frac{c}{d}$ называют равными, если справедливым является равенство $a\cdot d=b\cdot c$.
Обыкновенные дроби $\frac{a}{b}$ и $\frac{c}{d}$ называют неравными, если равенство $a\cdot d=b\cdot c$ не выполняется.
Выяснить, являются ли равными дроби $\frac{1}{3}$ и $\frac{2}{6}$.
Проверим, выполняется ли равенство $a\cdot d=b\cdot c$:
\[1\cdot 6=3\cdot 2.\]Равенство выполняется, значит, дроби $\frac{1}{3}$ и $\frac{2}{6}$ являются равными: $\frac{1}{3}=\frac{2}{6}$.
Данный пример можно рассмотреть на примере яблок: одно из двух одинаковых яблок разделено на три равные доли, второе -- на $6$ долей. При этом видно, что две шестых доли яблока составляют $\frac{1}{3}$ долю.
Проверить, являются ли равными обыкновенные дроби $\frac{3}{17}$ и $\frac{4}{13}$.
Проверим, выполняется ли равенство $a\cdot d=b\cdot c$:
\[3\cdot 13\ne 17\cdot 4;\] \[39\ne 58.\]Равенство не выполняется, значит, дроби $\frac{3}{17}$ и $\frac{4}{13}$ не равны: $\frac{3}{17}\ne \frac{4}{13}$.
При сравнении двух обыкновенных дробей, если выясняется, что они не равны, можно узнать, какая из них больше, а какая -- меньше другой. Для этого используют правило сравнения обыкновенных дробей: нужно привести дроби к общему знаменателю и затем сравнить их числители. У какой дроби числитель будет больше, та дробь и будет являться большей.
Дроби на координатном луче
Все дробные числа, которые отвечают обыкновенным дробям, можно отобразить на координатном луче.
Чтобы на координатном луче отметить точку, которая соответствует дроби $\frac{m}{n}$, необходимо от начала координат в положительном направлении отложить $m$ отрезков, длина которых составляет $\frac{1}{n}$ долю единичного отрезка. Такие отрезки получают при делении единичного отрезка на $n$ равных частей.
Чтобы отобразить на координатном луче дробное число, нужно единичный отрезок разделить на части.
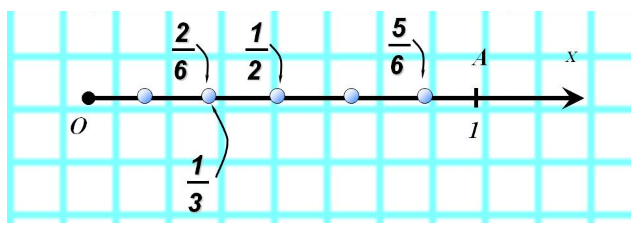
Рисунок 2.
Равные дроби описываются одним и тем же дробным числом, т.е. равные дроби представляют собой координаты одной и той же точки на координатном луче. Например, координатами $\frac{1}{3}$, $\frac{2}{6}$, $\frac{3}{9}$, $\frac{4}{12}$ описывается одна и та же точка на координатном луче, так как все записанные дроби равны.
Если точка описывается координатой с большей дробью, то она будет находится правее на горизонтальном направленном вправо координатном луче от точки, координатой которой является меньшая дробь. Например, т.к. дробь $\frac{5}{6}$ больше дроби $\frac{2}{6}$, то и точка с координатой $\frac{5}{6}$ находится правее точки с координатой $\frac{2}{6}$.
Аналогично, точка с меньшей координатой будет лежать левее точки с большей координатой.












