Как увидеть функцию?
Известно, что функция $y=f\left(x\right)$ представляет собой некоторый закон, по которому каждому числовому значению одной переменной $x$ ставится в соответствие определенное числовое значение другой переменной $y$.
В отличие от числовой оси, предназначенной для отображения отдельных чисел, именно системы координат на плоскости позволяют отображать функционально зависимые пары чисел $x$ и $y$.
Рассмотрим систему координат на плоскости, образованную двумя взаимно перпендикулярными осями, которые называются осями координат.
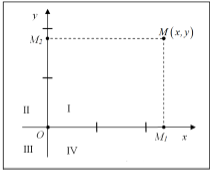
Точка пересечения осей координат называется началом координат и обозначается буквой O. Горизонтальная ось направлена слева направо, называется осью абсцисс и обозначается $Ox$. Вертикальная ось направлена снизу вверх, называется осью ординат и обозначается $Oy$. С целью указания числовых значений координат на обоих осях выбирають масштабную единицу (одинаковую или разную).
При указанных условиях расположение любой точки $M$ на плоскости полностью определяется её координатами. Для определения координат нужно спроектировать точку $M$ на оси $Ox$ и $Oy$, то есть опустити перпендикуляри $MM_{1} $ и $MM_{2} $ на эти оси. Первую координату $x$ (абсциссу) точки $M$ указывает положение точки $M_{1} $ на осі $Ox$. Вторую координату $y$ (ординату) точки $M$ указывает положение точки $M_{2} $ на осі $Oy$. То, что точка $M$ имеет своими координатами числа $x$ и $y$, записывают в виде $M\left(x,\; y\right)$.
Оси координат делят плоскость на четыре части, которые называются четвертями или квадрантами. Квадранти нумеруют римскими цифрами против часовой стрелки. Знаки координат в каждом из квадрантов следующие:
- I квадрант - $x>0,\; \; y>0$;
- II квадрант - $x0$;
- III квадрант - $x
- IV квадрант - $x>0,\; \; y
Точки на оси $Oy$ имеют координату $x=0$, точки на оси $Ox$ имеют координату $y=0$. Начало координат имеет нулевые значения обеих координат.
Обратная задача - построение точки $M$ по её заданным координатам $x$ и $y$ - решается посредством предварительного построения её проекций, то есть точек $M_{1} \left(x,\; 0\right)$ и $M_{2} \left(0,\; y\right)$ на осях $Ox$ и $Oy$ соответственно. Далее через эти точки следует провести прямые, перпендикулярные осям, и на их пересечении будет получена точка $M$.
Описанные координаты, которые применяются для определения положения точек на плоскости, называются прямоугольными. Их также называют декартовыми в честь французского учёного XVII века Рене Декарта, которого считают основателем аналитической геометрии.
Особенности поведения функций
Использование прямоугольной системы координат для графического отображения функций позволяет видеть характерные особенности их поведения.
Монотонность функции
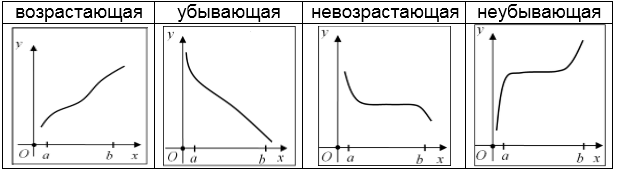
Рассмотрим функцию $y=f\left(x\right)$ на интервале $\left(a,\; b\right)$. Будем выбирать на нём произвольные точки $x_{1} y_{2} $), невозрастающей (если $ y_{1} \ge y_{2} $) и неубывающей (если $ y_{1} \le y_{2} $).
 Монотонность функции">
Монотонность функции">
Описанное поведение называется монотонностью функции на данном интервале. При этом возрастающие и убывающие функции называют строго монотонными.
Ограниченность функции
Рассмотрим функцию $y=f\left(x\right)$ на интервале $\left(a,\; b\right)$. Будем выбирать на нём произвольные точки $x^{*} $ и сравнивать значения $y^{*} =f\left(x^{*} \right)$ с некоторым заданным числом $M>0$. На этом интервале функция считается ограниченной, если справедливо неравенство $\left|y^{*} \right|\le M$.
График такой функции расположен в полосе между горизонтальными прямыми, проведёнными через точки $y=M$ и $y=-M$.
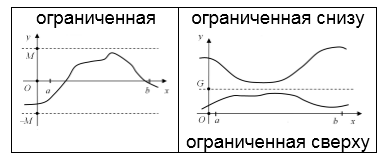
Рассмотрим функцию $y= \sin x$ и число $M=1$. Функция ограничена, так как значения $\left|\sin x\right|\le 1$ для любых $-\infty
На интервале $\left(a,\; b\right)$ функция считается ограниченной сверху или ограниченной снизу, если существует такое число $G$, что $y^{*} \le G$ или $y^{*} \ge G$ соответственно. При этом график функции располагается или под, или над горизонтальной прямой, проведённой через точку $y=G$.
Функция $y=\frac{1}{x} $ ограничена сверху на интервале $\left(-\infty ,\; 0\right)$, и ограничена снизу на интервале $\left(0,\; +\infty \right)$, причем в обоих случаях $G=0$, то есть соответствующие графики расположены ниже и выше оси $Ox$.
Четность и нечетность функции
Рассмотрим функцию $y=f\left(x\right)$ на интервале $\left(-a,\; a\right)$, симметричном относительно начала координат. Данная функция будет считаться четной на этом интервале, если справедливо равенство $f\left(-x\right)=f\left(x\right)$, и нечетной, если $f\left(-x\right)=-f\left(x\right)$. Если же ни одно из указанных условий не выполняется, то функция не относится ни к четным, ни к нечетным.
График четной функции симметричен относительно оси $Oy$, нечетной - относительно начала координат.
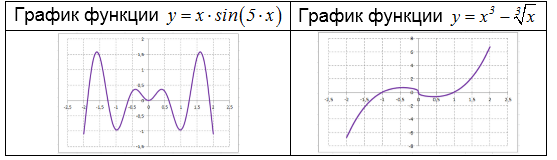
Проанализировать на четность (нечетность) функцию $y=x\cdot \sin \left(5\cdot x\right)$.
Заменим в функции $x$ на $-x$. Получим:
\[f\left(-x\right)=\left(-x\right)\cdot \sin \left(-5\cdot x\right)=\left(-x\right)\cdot \left(-\sin \left(5\cdot x\right)\right)=x\cdot \sin \left(5\cdot x\right)=f\left(x\right). \]Следовательно, данная функция четная. Её график симметричен относительно оси $Oy$.
Проанализировать на четность (нечетность) функцию $y=x^{3} -\sqrt[{3}]{x} $.
Заменим в функции $x$ на $-x$. Получим:
\[f\left(-x\right)=\left(-x\right)^{3} -\sqrt[{3}]{-x} =-\left(x^{3} \right)-\left(-\sqrt[{3}]{x} \right)=-\left(x^{3} \right)+\sqrt[{3}]{x} =-f\left(x\right). \]Следовательно, данная функция нечетная. Её график симметричен относительно начала координат.
Периодичность функции
Рассмотрим функцию $y=f\left(x\right)$ на интервале $\left(a,\; b\right)$. Данная функция будет считаться периодической на этом интервале, если существует некоторое постоянное число $T>0$, для которого $f\left(x\pm T\right)=f\left(x\right)$ при $a
Найти период функции $y=\sin \left(2\cdot x+5\right)$ при $ -\infty
Условие периодичности имеет вид $\sin \left(2\cdot \left(x+T\right)+5\right)=\sin \left(2\cdot x+5\right)$. По формуле для разности синусов получим $\sin T\cdot \cos \left(2\cdot x+5+T\right)=0$. Сомножитель $\sin T$ не зависит от $x$, и поэтому уравнение $\sin T=0$ дает значение основного периода $T=\pi $. Из уравнения $\cos \left(2\cdot x+5+T\right)=0$ значение периода, независимого от $x$, получить невозможно.
Способы задания функции
Кроме графического и аналитического способов задания функции, использованных выше, существует еще и табличный.
При табличном способе в определенном порядке выписываются значения аргумента $x_{1} ,\; x_{2} ,\; \ldots ,\; x_{n} $ и соответствующие значения функции $y_{1} ,\; y_{2} ,\; \ldots ,\; y_{n} $. В таком виде часто получают функции во время измерительных экспериментов. Кроме того, таблицы значений разнообразных специальных функций мы можем видеть в справочниках.
Форма аналитического способа задания функции может быть явной, неявной и параметрической.
Если функция $y$ аргумента $x$ имеет вид уравнения, разрешенного относительно $y$, то есть $y=f\left(x\right)$, то такая форма аналитического задания называется явной. Примеры представлены в задачах выше.
Если аргумент $x$ и функция $y$ связаны между собой уравнением, не разрешенным относительно $y$, то есть в виде $F\left(x,\; y\right)=0$, то такая форма аналитического задания называется неявной. Например, $y^{2} +\cos \left(x+y\right)=0$.
Если соответствующие значения аргумента $x$ и функции $y$ связаны между собой через третью вспомогательную переменную (параметр) $t$, то есть $x=x\left(t\right)$ и $y=y\left(t\right)$, то такая форма аналитического задания называется параметрической. Например, $x=2\cdot tgt$, $y=5\cdot \cos t$.











