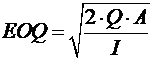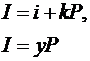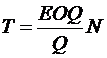Задачи управления входящим товарным потоком
Входящий товарный поток – поток сырья, материалов, полуфабрикатов, комплектующих, готовой продукции, поступающий на предприятие из внешних источников с целью использования в производственном процессе или для перепродажи.
Управление входящим товарным потоком предполагает решение следующих задач:
- прогнозирование величины входящего товарного потока на основе потребностей производства с учетом факторов сезонности спроса;
- определение оптимальной партии заказа товара;
- определение оптимальной периодичности поставок;
- расчет и анализ издержек на управление входящим товарным потоком;
- управление приемкой входящего товарного потока;
- контроль качественных и количественных параметров потока;
- управление размещением входящего потока на складе и хранением.
Определение оптимальной величины и периодичности входящего товарного потока
Формирование логистической системы управления входящим товарным потоком предполагает определение двух ключевых параметров: размер заказываемой партии и периодичность поставок. Оптимальными будут те параметры, которые позволяют достичь минимума совокупных логистических издержек на управление входящим потоком.
На выбор размера партии поставки влияют следующие факторы:
- величина затрат на хранения материалов,
- издержки оформления заказов на закупки,
- оптовые и транспортные скидки.
Закупки малыми партиями позволяют сократить издержки хранения товаров на складе, вместе с тем в данном случае увеличиваются частота поставок и соответственно возрастают затраты на оформление заказов и экспедирование поставок. Закупки крупными партиями зачастую позволяют получить оптовые скидки. Оптимальным размером заказа является величина партии материалов, которая позволит сократить до минимума общую сумму совокупных расходов на поставку и хранение материалов.
Методика оптимизации размера заказа заключается в сравнении преимуществ и недостатков приобретения материалов большими и малыми партиями и в выборе размера заказа, соответствующего минимальной величине общих расходов на пополнение запасов.
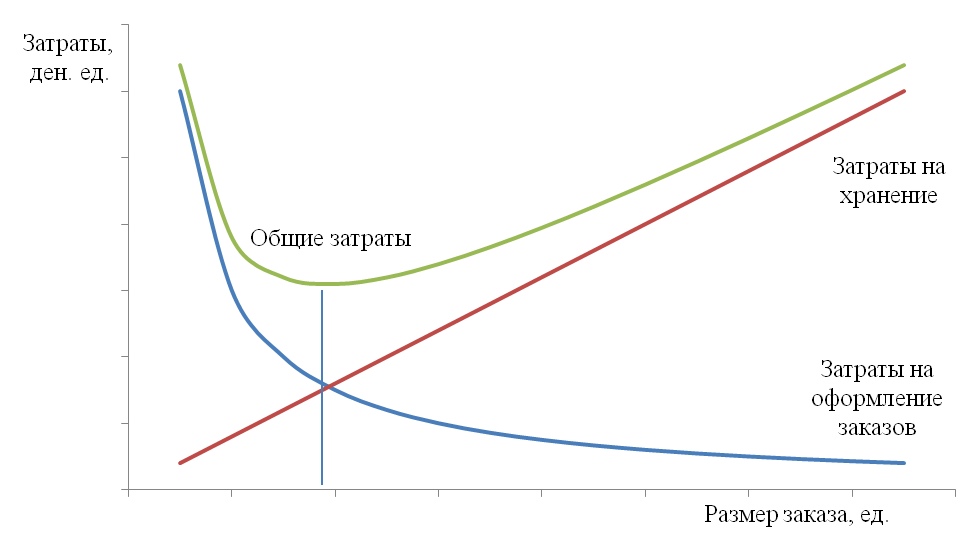
Классическая зависимость затрат на запасы от размера заказа представлена на рис. 1.
На графике видно, что затраты на хранение запаса возрастают при увеличении партии поставки, а затраты на оформление заказов сокращаются. Оптимальной партией поставки будет та, при которой совокупные затраты принимают минимальное значение.
Классическая модель нахождения оптимального размера заказа, широко цитируемая в специальной литературе по логистике, носит названия формула Уилсона (другие названия – формула $EOQ$, модель Харриса-Уилсона).
Согласно формуле Уилсона, оптимальный размер заказа рассчитывается:
где $Q$ – прогнозная потребность в товаре на определенный период (год), ед.; $I$ – стоимость хранения единицы товара в год, ден. ед.; $A$– стоимость оформления заказа, ден. ед.
Стоимость хранения единицы товара ($I$) рассчитывают исходя из складских затрат, стоимости запаса, а также издержек обесценивания товара в процессе хранения. В литературе встречаются следующие выражения для расчета удельных затрат на хранение:
где $i$ − складские издержки хранения единицы запаса, ден.ед; $k$ − издержки обесценивания товара в процессе хранения, %; $P$ – цена единицы запаса, ден.ед; $y$ − издержки хранения единицы запаса, % от стоимости запаса.
Если общая потребность в единичный период времени составляет $Q$ единиц, а восполнение этой потребности ведется партиями по $EOQ$ единиц, то отношение $Q / EOQ$ определяет оптимальное количество заказов в единичный период, а оптимальный интервал времени между заказами (в днях) можно найти по формуле:
где $N$ – число дней в плановом периоде.