Логические операции и их свойства

Конъюнкция или логическое умножение (в теории множеств – это пересечение)

Конъюнкция является сложным логическим выражением, которое истинно в том и только том случае, когда оба простых выражения являются истинными. Такая ситуация возможно лишь в единственном случае, во всех остальных случаях конъюнкция ложна.

Обозначение: &, $\wedge$, $\cdot$.

Таблица истинности для конъюнкции

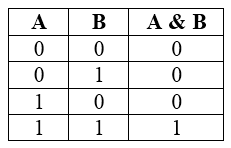
Рисунок 1.

Свойства конъюнкции:

1. Если хотя бы одно из подвыражений конъюнкции ложно на некотором наборе значений переменных, то и вся конъюнкция будет ложной для этого набора значений.
2. Если все выражения конъюнкции истинны на некотором наборе значений переменных, то и вся конъюнкция тоже будет истинна.
3. Значение всей конъюнкции сложного выражения не зависит от порядка записи подвыражений, к которым она применяется (как в математике умножение).

Дизъюнкция или логическое сложение (в теории множеств это объединение)

Дизъюнкция является сложным логическим выражением, которое истинно практически всегда, за исключением, когда все выражения ложны.

Обозначение: +, $\vee$.

Таблица истинности для дизъюнкции

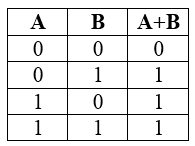
Рисунок 2.

Свойства дизъюнкции:

1. Если хотя бы одно из подвыражений дизъюнкции истинно на некотором наборе значений переменных, то и вся дизъюнкция принимает истинное значение для данного набора подвыражений.
2. Если все выражения из некоторого списка дизъюнкции ложны на некотором наборе значений переменных, то и вся дизъюнкция этих выражений тоже ложна.
3. Значение всей дизъюнкции не зависит от порядка записи подвыражений (как в математике – сложение).

Отрицание, логическое отрицание или инверсия (в теории множеств это отрицание)

Отрицание - означает, что к исходному логическому выражению добавляется частица НЕ или слова НЕВЕРНО, ЧТО и в итоге получаем, что если исходное выражение истинно, то отрицание исходного – будет ложно и наоборот, если исходное выражение ложно, то его отрицание будет истинно.

Обозначения: не $A$, $\bar{A}$, $¬A$.

Таблица истинности для инверсии

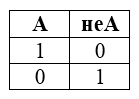
Рисунок 3.

Свойства отрицания:

«Двойное отрицание» $¬¬A$ является следствием суждения $A$, то есть имеет место тавтология в формальной логике и равно самому значению в булевой логике.

Импликация или логическое следование

Импликация - это сложное логическое выражение, которое истинно во всех случаях, кроме как из истины следует ложь. То есть, данная логическая операция связывает два простых логических выражения, из которых первое является условием ($A$), а второе ($A$) является следствием условия ($A$).

Обозначения: $\to$, $\Rightarrow$.

Таблица истинности для импликации

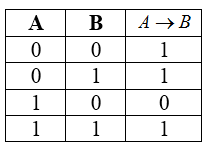
Рисунок 4.

Свойства импликации:

1. $A \to B = ¬A \vee B$.
2. Импликация $A \to B$ ложна, если $A=1$ и $B=0$.
3. Если $A=0$, то импликация $A \to B$ истинна при любом значении $B$, (из лжи может следовать истинна).

Эквивалентность или логическая равнозначность

Эквивалентность - это сложное логическое выражение, которое истинно на равных значениях переменных $A$ и $B$.

Обозначения: $\leftrightarrow$, $\Leftrightarrow$, $\equiv$.

Таблица истинности для эквивалентности

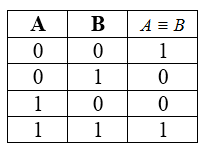
Рисунок 5.

Свойства эквивалентности:

1. Эквивалентность истинна на равных наборах значений переменных $A$ и $B$.
2. КНФ $A \equiv B = (\bar{A} \vee B) \cdot (A \cdot \bar{B})$
3. ДНФ $A \equiv B = \bar{A} \cdot \bar{B} \vee A \cdot B$

Строгая дизъюнкция или сложение по модулю 2 ( в теории множеств это объединение двух множеств без их пересечения)

Строгая дизъюнкция истинна, если значения аргументов не равны.

Для функции трёх и более переменных результат выполнения операции будет истинным только тогда, когда количество аргументов равных $1$, составляющих текущий набор — нечетное. Такая операция естественным образом возникает в кольце вычетов по модулю 2, откуда и происходит название операции.

Обозначения: $A \oplus B$ (в языках программирования), $A≠B$, $A \wedge B$ (в языках программирования).

Таблица истинности для операции сложения по модулю два

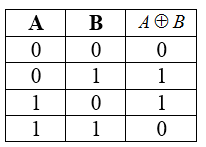
Рисунок 6.

Свойства строгой дизъюнкции:

• $a \oplus 0 = a$(идемпотентность)
• $a \oplus 1 = \bar{a}$(отрицание)
• $a \oplus a = 0$(получение 0)
• $a \oplus b = b \oplus a$(коммутативность)
• $(a \oplus b) \oplus c = a \oplus (b \oplus c)$(ассоциативность)
• $(a \oplus b) \oplus b = a$(поглощение)
• $\bar{a} \oplus b = a \oplus \bar{b} = (a \equiv b)$(сравнения по модулю)

Стрелка Пирса

Бинарная логическая операция, булева функция над двумя переменными. Названа в честь Чарльза Пирса и введена в алгебру логики в $1880—1881$ гг.

Обозначения: $\downarrow$ , ИЛИ-НЕ

Таблица истинности для стрелки Пирса

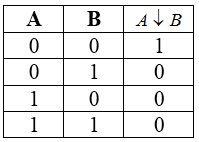
Рисунок 7.

Свойства:

Стрелка Пирса, как и конъюнкция, дизъюнкция, отрицание, образует базис для булевых функций двух переменных. При помощи стрелки Пирса, можно построить все остальные логические операции, например:

$X \downarrow X = ¬X$— отрицание

$(X \downarrow Y) \downarrow (X \downarrow Y) \equiv X \vee Y$ — дизъюнкция

$(X \downarrow X) \downarrow (Y \downarrow Y) \equiv X \wedge Y$ — конъюнкция

$((X \downarrow X) \downarrow Y) \downarrow ((X \downarrow X) \downarrow Y) = X \to Y$ — импликация

В электронике стрелка Пирса представлена в виде элемента, который носит название «операция 2ИЛИ-НЕ» (2-in NОR).

Штрих Шеффера

Булева функция двух переменных или бинарная логическая операция. Введена в рассмотрение Генри Шеффером в 1913 г.

Обозначения: $|$, эквивалентно операции И-НЕ.

Таблицей истинности для функции штрих Шеффера

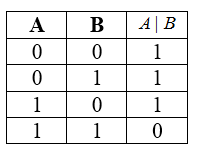
Рисунок 8.

Свойства:

Штрих Шеффера образует базис для всех булевых функций двух переменных. Применяя штрих Шеффера можно построить остальные операции, например,

$X \mid X = ¬X$ — отрицание

$(X \mid Y) \mid (X \mid Y) = (X \wedge Y)$ — конъюнкция

$(X \mid X) \mid (Y \mid Y) = X \vee Y$ — дизъюнкция

$X \mid ¬X$ — константа 1

Для электроники это означает, что реализация схем возможна с использованием одного типового элемента (правда это дорогостоящий элемент).

Порядок выполнения логических операций в сложном логическом выражении

1. Инверсия(отрицание);
2. Конъюнкция (логическое умножение);
3. Дизъюнкция и строгая дизъюнкция (логическое сложение);
4. Импликация (следствие);
5. Эквивалентность (тождество).

Для того чтобы изменить указанный порядок выполнения логических операций, необходимо использовать скобки.

Общие свойства

Для набора из $n$ логических переменных существует ровно $2^n$ различных значений. Таблица истинности для логического выражения от $n$ переменных содержит $n+1$ столбец и $2^n$ строк.