Силы отталкивания, притяжения и образование химической связи
Между молекулами действуют силы притяжения, вызванные взаимодействием постоянных диполей полярных связей, а также индуцированными диполями. Действие сил притяжения влияет на химические свойства соединений.
Силы притяжения способствуют образованию молекулярных кристаллов и жидкостей, увеличивают скорость химической реакции.
При дальнейшем сближении молекул, начинают действовать силы отталкивания между заполненными валентными оболочками. В равновесных системах между силами притяжения и отталкивания наблюдается равновесие, а минимальное расстояние, на которое могут сблизиться молекулы, определяется ван-дер-ваальсовыми радиусами атомов.
Но, возможны ситуации, когда расстояние между молекулами становится меньше, чем ван-дер-ваальсовы радиусы (например, при конденсации пара в жидкость и твердое тело). Это указывает на то, что между молекулами устанавливается химическая связь. Образовавшаяся связь может быть слабой, средней силы или сильной.
В результате реакции циклоприсоединения циклопентадиен $C_5H_6$ быстро превращается в димер $C_{10}H_{12}$ при хранении. Нагревание димера ведет к отгонке первоначального мономерного циклопентадиена, то есть при средних температурах наблюдается динамическое равновесие между молекулой димера и $2$ молекулами циклопентадиена. В жидком образце циклопентадиена $1$ и $1`$ и $4$ и $2`$ могут сближаться на расстояние, которое намного меньше, чем сумма ван-дер-ваальсовых радиусов.
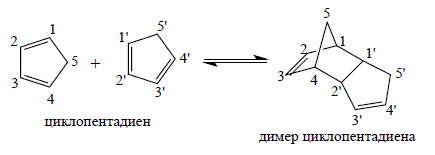
Рисунок 1.
Между атомами $1$ и $1'$ и $4$ и $2'$ образуются прочные ковалентные связи $\sigma $-типа.
Динамика реакции получения димера
Динамика реакции получения димера циклопентадиена выглядит следующим образом. Между молекулами циклопентадиена, которые удалены друг от друга на достаточно значительное расстояние, действуют силы притяжения. Так как молекулы неполярны, то притяжение происходит за счет слабых взаимодействия, связанных с дисперсионными силами. Допустим, дисперсионные силы привели к появлению молекулярных пар $(C_5H_6^.C_5H_6)$, в которых расстояние между молекулами соответствует ван-дер-ваальсовым радиусам.
В какой-то момент времени среди этих пар часть будет устроена таким образом, что атомы $1$ и $1'$ и $4$ и $2'$ окажутся в ван-дер-ваальсовом контакте. В результате некоторые из этих ориентированных пар молекул приобретут энергию, необходимую для преодоления энергетического барьера, после чего станет возможным протекание реакции.
Непрореагировавшие пары молекул в результате теплового движения могут распасться, потом снова дать новые пары. Часть новых пар будет подходяще ориентирована, все время будет увеличиваться степень димеризации, но часть молекул димера будут вновь распадаться на мономерные молекулы. Таким образом, установится положение равновесия, соответствующее температуре образца.
Нарушение равновесия молекула-димер
Молекулы одного и того же соединения могут принимать участие в различных равновесиях.
В жидком состоянии возможно существование двух и более разных молекулярных форм, они могут быть конформерами, как в $1,2$-дибромэтане, или таутомерами, как в ацетилацетоне. Каждая из форм имеет свой индивидуальный спектр полос поглощения.
Любой сдвиг в таком равновесии, который может быть обусловлен либо изменениями концентрации и температуры или взаимодействием с растворителем, отражается на спектральных изменениях, что справедливо и для ультрафиолетовой и инфракрасной спектроскопии, и по отношению к ядерному магнитному резонансу.
Важным равновесным состоянием является ассоциация молекул растворенного вещества. Равновесие сильно подвержено влиянию как природы растворителя, так и концентрации растворенного вещества.
Карбоновые кислоты в виде чистой жидкости и в твердом состоянии существуют в форме димеров, при этом внутри каждой пары молекул образуются достаточно сильные водородные связи. При разбавлении неполярным растворителем до низкой концентрации происходит установление равновесия мономер -- димер, которое существенно сдвинуто в сторону образования димера.
В полярном растворителе $(CHCl_3$ или $CH_3CN)$ при той же концентрации получает сильное преимущество более полярная мономерная форма.

Рисунок 2.
Самоассоциация молекул
Молекулы, содержащие $O-H, N-H, C-H, S-H$ и др. группы, склонны к образованию самоассоциатов в чистом виде, в растворах инертных растворителей, в газовой фазе. При этом могут быть установлены различные типы равновесий: мономер-димер, мономер -- тример, $\dots$ , мономер-n-мер.
Образовавшийся самоассоциат может быть линейным или циклическим. Для ассоциации мономер-n-мер справедливо отношение
Константа равновесия $K_n$, выраженная в мольных долях, может быть задана уравнением:
где $n$ - порядок самоассоциации; $A_0,A_n\ $-- начальная и равновесная концентрация вещества $A$, выраженная в мольных долях.
Величина наблюдаемого химического сдвига линейного типа имеет вид
для циклического самоассоциата
где ${\delta }_1,\ {\delta }_n$ -- химические сдвиги вещества \textit{А} в мономерной и n-мерной формах; $\alpha =\frac{A_n}{A_0}$ -- степень самоассоциации; ${\triangle }_n={\delta }_n-{\delta }_1$- разность химических сдвигов n-мера и сигнала мономера.
При использовании данных уравнений для нахождения величин $K_n$ и ${\triangle }_n$ используют различные приближения:
-
Метод предельного наклона. Этот метод разработал Шулери., он позволяет из наклона кривой концентрационной зависимости, экстраполированной к бесконечному разбавлению, определить величину $\ {\triangle }_nK_n$. В случае самоассоциации с $n=2$ наклон зависимости химических сдвигов от концентрации в точке $A_0=0$ не равен нулю.
Метод предельного наклона позволяет определить, протекающий в системе процесс димеризации, но не позволяет найти отдельно друг от друга параметры $K_n$ и величину $\ {\triangle }_n$.
-
Метод Липперта. Этот метод основывается на допущении, что существует единственный тип ассоциативного равновесия в определенном концентрационном интервале. Графическим методом определить параметры ${n,\triangle }_n,K_n$ можно определить по уравнению
\[\sqrt[n]{\frac{\delta -{\delta }_1}{A^{n-1}_0}}=\sqrt[n]{nK_n{\triangle }_n}-\sqrt[n]{nK_n{\triangle }^{1-n}_n}\left(\delta -{\delta }_1\right).\]Методы предельного наклона и Липперта позволяют точно определить порядок ассоциации.












