Известно, что природный метан имеет форму тетраэдра. Форма плоского квадрата для его молекулы не характерна и энергетически не выгодна. Однако МО такого плоского метана можно построить.
Чтобы построить МО плоского метана, удобно разложить молекулу на два фрагмента: центральный атом углерода и периметрическую $H_4$ группу:

Рисунок 1.
Орбитали последней получают по схеме двухорбитального взаимодействия, исходя из орбиталей двух $H_2$ групп) в которых атомы водорода удалены друг от друга на соответствующее расстояние.
МО плоского метана можно составить из кобинации орбитали углерода и групповой орбитали фрагмента $H_4$. Молекулярные орбитали плоского $H_4$ со связями, направленными к центру квадрата, строиятся путем возмущения связующих и разрыхляющих $\sigma$ и $\sigma$*-орбиталей молекул $H_2$ (рис. 1).
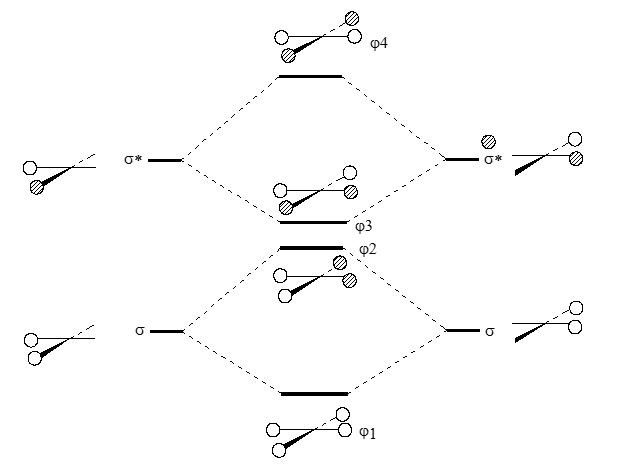
Рисунок 2. Диаграмма орбиталей для квадратной молекулы $H_4$
После чего квадрат растягивается, расстояния $H-H$удлиняются; тогда все связующие и разрыхляющие орбитали ансамбля $H_4$ уменьшаются и преобретают примерно равную энергию, близкую к энергии орбиталей $\varphi_2$ и $\varphi_3$ на рис. 1.
$\varphi_3$ и $\varphi_4$ орбитали имеют по одному узлу и совмещаются друг с другом. Как и соответствующие МО тетраэдрической формы, их можно представить и в иной форме с узловыми плоскостями, проходящими через вершины квадрата:
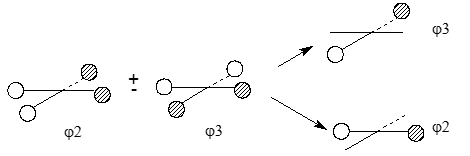
Рисунок 3.
Оба представления полностью идентичны, но симметрия МО, представленных справа, хорошо адаптирована к симметрии МО $C2p_x$ и $C2p_y$. Поэтому при построении МО диаграммы плоского метана используют второе представление.
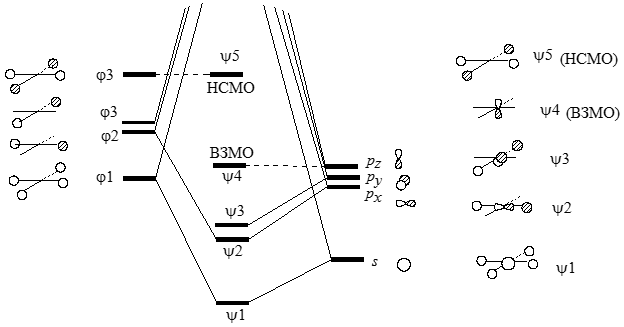
Рисунок 4. Диаграмма орбитального взаимодействия для молекулы плоского метана
На рис. 2. изображены пять из восьми валентных МО плоского метана. В молекуле $CH_4$ связывание может осуществляться четырьмя парами валентных электронов. В тетраэдрической форме метана все эти электроны участвуют в образовании связей $C-H$: на каждую связь по два электрона. Однако в плоской форме метана в образовании этих связей участвуют только три пары электронов. Эти заполненные МО обозначены как $\psi$1, $\psi$2 и $\psi$3 (орбитали $\psi$2 и $\psi$3 будут вырождеными).
Оставшаяся пара электронов находится на несвязывающей $p$-орбитали $\psi_4$ ($p_z$), перпендикулярной плоскости молекулы. Таким образом, высшая занятая молекулярная орбиталь плоского метана ($\psi_4$) имеет характер неподеленной пары. МО плоского метана ($\psi_5$) - это групповая орбиталь $\varphi_4$. Она имеет две узловые плоскости. У атома углерода нет низко лежащих МО с двумя узловыми плоскостями, поэтому уровень $\varphi_4$ не может расщепиться на связующий и разрыхляющий.
Геометрическое строение плоского метана
Однозначно изобразить геометрическое строение плоского метана с помощью обычных структурных формул довольно сложно. Вероятно, лучше всего рассматривать такую плоскую молекулу метильный карбанион $CH^{3-}$, протонированный не по р-орбитали углерода, которая несет отрицательный заряд, а по $\sigma$-связи $C-H$:
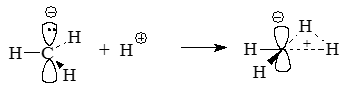
Рисунок 5.
Плоский метан должен стабилизироваться, если вместо одного из водородов в молекулу ввести $\pi$-акцепторнй ($-M$) или $\sigma$-донорный ($+I$) заместитель. Первый будет уменьшать дефицит электронов $\sigma$-остова молекулы. Особенно эффективно введение атомов лития, который обладает сильными ($-M$) и ($+I$)-эффектами.
Тетракоординированные системы
По аналогии с постраением МО плоского метана возможно построить и МО других тетракоординированных систем. В частности молекул гидридов с общей формулой $AH_4$ .
Для таких молекул сначала строят МО плоской молекулы, а затем, деформируют плоскую структуру, и рассмотривают, как реагирует на эту деформацию энергетический уровень и форма отдельной МО:

Рисунок 6.
Корреляционная диаграмма молекулярных орбиталей для таких систем $AH_4$ показана на рис. 3
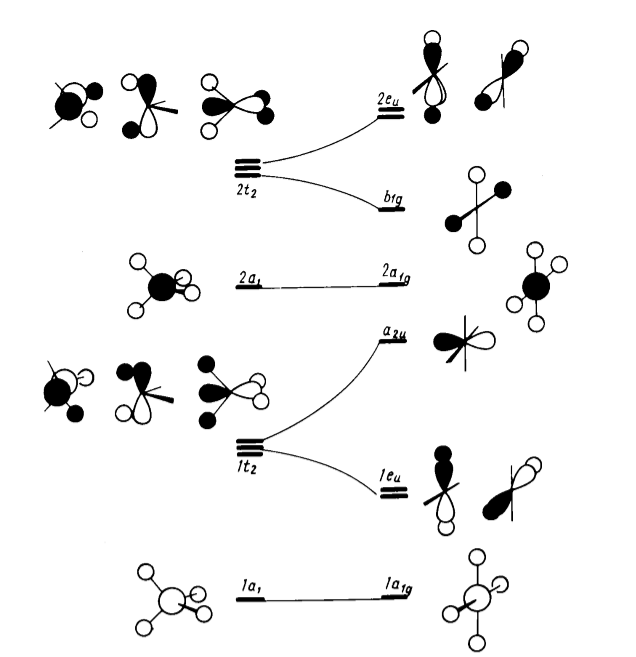
Рисунок 7. Диаграмма Уолша для искажения молекул $AH_4$












