В предыдущих главах на примерах простых молекул было показаны построения молекулярных орбиталей при помощи диаграмм орбитальных взаимодействий. Анализируя формы и энергии граничных МО, можно решать множества вопросов, которые связанны со строениями и реакционными способностями данных молекул. Примеры таких применений теории МО будут и будут рассмотрены далее.
Наблюдаемые взаимодействия (корреляции) можно разделить на три категории, существенно различающиеся по физической природе. Это взаимодействия через спин-спиновую связь, взаимодействия через пространство и через химический обмен. Первая из них, подразделяется на гомоядерное (например $H-H$) и гетероядерное (например, между ядрами $H-C$) взаимодействия. С ее помощью удается идентифицировать структурные фрагменты молекулы и объединить их в нечто целое. Взаимодействие через пространство является основой ядерного эффекта Оверхаузера. Наиболее часто он используется для выяснения стереохимии и конформационного состояния молекулы. Этот метод целесообразно использовать только после установления основных деталей химического строения молекулы, поскольку различия в строении могут полностью изменить интерпретацию корреляций.
Главная цель построений диаграммы орбитального взаимодействия заключается в нахождении и анализе граничных орбиталей и объяснении этих орбитальных взаимодействий, которые и контролируют формы граничных молекулярных орбиталей. МО отдельных групп взаимодействовуют не только прямым путем "через пространство", но и в обход - через $\sigma $-связи.
Взаимодействие через пространство. Спин-спиновое взаимодействие
Взаимодействие через пространство разделяеться на косвенное спин-спиновое взаимодействие и прямое спин-спиновое взаимодействие.
Рассмотрим этот тип взаимодействия на примере двухатомной молекулы, содержащей магнитные ядра различных элементов - $HF$. Магнитный момент ядра $H$ вызывает слабую магнитную поляризацию связующих электронов, которая передается через орбитали перекрывающихся на ядро $HF$. В результате внешнее магнитное поле, действующее на ядро $HF$, будет несколько возрастать или уменьшаться (в зависимости от ориентации ядра $H$ - ($\alpha $ или $\beta $).
Таким образом, в результате двух различных значений локального магнитного поля, определяет резонансную частоту ядра $F$, приведет к расщеплению сигнала $F$ в дублет. Поскольку это влияние является взаимным, то подобный эффект возникнет и на ядре $H$.
Вследствие практически одинаковой заселенности уровней, два спиновых состояния ядра $H$ одинаково вероятны, поэтому компоненты дублетного сигнала имеют одинаковую интенсивность. Состояние с меньшей энергией соответствует антипараллельной ориентации ядерного и электронного магнитных моментов. Передача магнитной поляризации подчиняется принципу Паули и правилу Хунда.
Принцип Паули: два электрона не могут находиться в одинаковом квантовом состоянии (на одной молекулярной орбитали не может быть два электрона с одинаковым спином).
Правило Хунда: при заполнении электронами орбиталей определенного подуровня модуль их суммарного спинового квантового числа должно быть максимально возможным.
Спин-спиновое взаимодействие пропорционально произведению гиромагнитных отношений ядер. Количественно спин-спинового взаимодействия характеризуют константой спин-спинового взаимодействия ($J$) - фактически это расстояние между компонентами мультиплетного сигнала, если же расщепление связано с различным химическим сдвигом, то эта расстояние меняться.
Диаграмма энергетических уровней двоспиновой системы
При отсутствии спин-спинового взаимодействия ($JAB = 0$) получаем $4$ различных состояния для двух ядер ($A$ и $B$) во внешнем магнитном поле $Bz$:
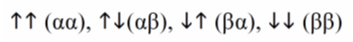
Рисунок 1.
Это означает, что оба ядерные магнитные моменты могут быть ориентированы либо параллельно, либо антипараллельно. Диаграмму энергетических уровней для двоспиновои системы можно представить так:
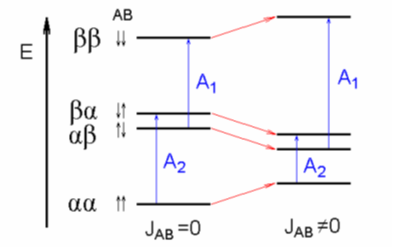
Рисунок 2.
Если спин-спиновое взаимодействие отсутствует ($JAB = 0$), то переходы $A_1$ и $A_2$ для ядра $A$ имеют одинаковую энергию. Если же есть спин-спиновое взаимодействие ($JAB ≠ 0$), то отдельные состояния ($\alpha $$\beta $ и $\beta $$\alpha $) спиновой системы стабилизируются (энергия снижаются), а другие ($\alpha $$\alpha $ и $\beta $$\beta $) - дестабилизируются (энергия повышается) в соответствии с относительной ориентацией магнитных моментов. Принято считать, что при положительном знаке константы ($JAB > 0$) ниже энергетическое состояние соответствует антипараллельными ориентации ядерных моментов. Поэтому, при наличии спин-спинового взаимодействия переходы $A_1$ и $A_2$ для ядра $A$ иметь различные значения энергии.
Антипараллельными ориентация ядерных моментов была принята как отвечающая ниже энергетическом состояния при $JAB > 0$. Поэтому состояния $\alpha $$\beta $ и $\beta $$\alpha $ стабилизировались, а состояния $\alpha $$\alpha $ и $\beta $$\beta $ дестабилизировались. Для ясности на вышеупомянутом рисунке показано только переходы для одного ядра ($A$). Количественное трактовки спин-спинового взаимодействия в случае системы $AB$ (то есть для двух ядер - $A$ и $B$) достаточно простое, потому что собственные значения энергии спиновой системы легко рассчитать, используя простые формулы. Энергия соответствующих состояний в единицах частоты $v_A$ $i$ $v_B$ и константы спин спинового взаимодействия $JAB$ выражается такими уравнениями:
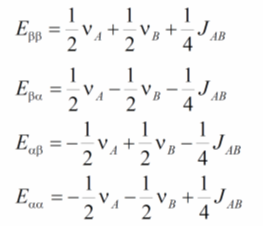
Рисунок 3.
Знак константы спин-спинового взаимодействия
По определению константа спин-спинового взаимодействия считается положительной, если нижнее энергетическое состояние имеет антипараллельную ориентацию ядерных моментов (как показано на рисунке выше). Если же справедливо обратное, то константа считается отрицательной. Согласно концепции магнитной поляризации ориентация спинов ядер различна в зависимости от числа связей. В случае нечетного числа связей антипараллельными ориентация спинов ядер имеет несколько ниже энергию по сравнению с параллельной. Поэтому существует обобщенное правило, согласно которому константы спин-спинового взаимодействия через четное число связей являются отрицательными, а через нечетное - положительными. Тот факт, что спин-спиновое взаимодействие передается через химические связи, делает константу $J$ очень чувствительной к типам связей, участвующих в передаче, и к их взаимной пространственной ориентации в молекуле. Вращения вокруг простых связей делает невозможным вращения вокруг кратных связей или заторможенной структуры и может привести к разнице констант для химически эквивалентных атомов (для последнего случая) и делает их магнитно-неэквивалентными.
Представление о магнитной эквивалентности
Магнитно-эквивалентные - это такие ядра, которые имеют одинаковую резонансную частоту и общее для всех характеристическое значение константы спин-спинового взаимодействия с ядрами любой соседней группы.
Изохроны - это ядра, которые имеют одинаковую резонансную частоту, однако могут иметь разные значения константы спин-спинового взаимодействия с ядрами соседних групп. Часто изохроны является химически эквивалентными, то есть имеют одинаковое химическое окружение. Однако химически эквивалентные ядра не всегда магнитно-эквивалентны. Протоны метильной группы являются магнитно-эквивалентными, потому что в результате свободного вращения вокруг связи $C-C$ все три протона приобретают одинаковые (усредненные во времени) резонансные частоты. И константы их спин-спинового взаимодействия с протонами соседней группы аналогичным образом одинаковы для всех трех протонов метильной группы, потому что все возможные конформации (а, б и в - см. рисунок ниже) одинаковые по энергии и одинаково заселены:
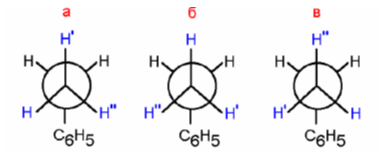
Рисунок 4.
Поэтому геометрические соотношения между метильными протонами и соседями, определяющих величину спин-спинового взаимодействия, становятся одинаковыми для каждого из них.











