Первый постулат Бора и размер атома водорода
Ранее (см. "Атомные орбитали") уже говорилось, что в свое время, пытаясь усовершенствовать планетарную модель атома, чтобы объяснить линейчатый характер спектров простых веществ, в частности - водорода, Н.Бор постулировал, что энергия электронов в атоме квантуется, т.е. изменяется скачкообразно. При этом каждому энергетическому уровню соответствует круговая орбита, по которой электрон вращается вокруг ядра. В классической механике вращательного движения существует понятие момента импульса $mvr$ (где $m$ - масса объекта, $v$ - скорость его движения, $r$ - радиус кривизны его траектории, который является постоянным в случае движения по поверхности сферы). По теории Бора, момент импульса электрона равен целому числу $n$ (это уже известное нам главное квантовое число) квантов энергии $\frac{h}{2\pi }$, где $h$ - постоянная Планка. Математическим выражением этого постулата является равенство:
$mvr=n\frac{h}{2\pi }$ (1)
из которого следует, что момент импульса тоже квантуется. С точки зрения теории Бора это связано с тем, что каждому энергетическому уровню соответствует определенный радиус орбиты, по которой электроны, обладающие энергией этого уровня, вращаются вокруг ядра.
Кроме радиуса, неизвестным в нашем уравнении является скорость. Ее можно найти из условия равенства центробежной и центростремительной сил в системе ядро-электрон. Центробежная сила равна $\frac{mv^2}{r}$. Центростремительная сила определяется взаимодействием ядра и электрона как двух одинаковых разноименных зарядов по закону Кулона и составляет $\frac{e^2}{r^2}$, где е - заряд электрона и протона, которые у них одинаковы по абсолютной величине. При условии равенства центробежной и центростремительной сил у атома водорода в основном состоянии:
$\frac{mv^2}{r}=\frac{e^2}{r^2}$ (2)
Решая систему уравнений (1) и (2) относительно $r$ и $v$, найдем, что
$r=\frac{h^2}{4{\pi }^2me^2}n^2$ (3)
$v=\frac{2\pi e^2}{nh}$ (4)
Подставляя в уравнение (3) $h = 6,63\times 10-34 Дж^*с$, $m = 9,11\times 10-31 кг$, $e = 1,602\times 10-19 Кл$ и $n=1$, получим $r = 0,053 нм$. Эта величина называется первым боровским радиусом и соответствует «границе» атома водорода в основном состоянии. Очевидно, второй, третий и т.д. боровские радиусы будут в $n^2$ раз больше первого.
Для дальнейших рассуждений представляет интерес формула кинетической энергии электрона. Подставляя выражение для скорости (4) в формулу кинетической энергии, получаем
$E=\frac{mv^2}{2}=-\frac{2{\pi }^2me^4}{h^2n^2}$ (5)
В случае водородоподобного иона, в котором электрон движется вокруг ядра, обладающего произвольным зарядом $Z$, кратным по абсолютной величине и противоположным по знаку заряду электрона, энергия возрастает в $Z^2$ раз и ее выражение принимает вид:
$E=-\left(2{\pi }^2mZ^2e^4\right)\left(h^2n^2\right)$ (6)
Очевидно, что кинетическая энергия электрона убывает обратно пропорционально $n^2$.
Размеры и форма орбиталей
Более подробную информацию о строении атома, учитывающую двойственный характер природы электрона и принцип неопределенности, можно получит из решения уравнения Шредингера. Для одноэлектронных систем типа атома водорода оно может быть произведено аналитически без каких-либо вспомогательных приближений. При этом атом удобно рассматривать в сферических координатах, начало которых расположено в центре тяжести ядра. Тогда каждому электрону будет соответствовать радиус-вектор с координатами $r$ (расстояние между электроном и ядром), $\theta $ (угол наклона) и $\varphi $ (угол поворота), а решение уравнения Шредингера можно будет искать в виде произведения двух функций, одна из которых зависит только от $r$, а другая - от углов $\theta $ и $\varphi $.
$\Psi =R\left(r\right)\Theta \left(\theta ,\varphi \right)$ (7)
Не останавливаясь подробно на всех выкладках, отметим, что решение уравнения Шредингера в полярных координатах удовлетворит краевому условию $R(\infty) = 0$, если энергия электрона соответствует формуле (5)
Рассмотрим волновые функции $\Psi $, получающиеся при $n=1$ и $n=2$.
При $n=1$ и $l=0$ $\Theta $ становится постоянным числом, не зависящим ни от $r$, ни от $\theta $, ни от $\varphi $ и $\Psi = R$. При $n=1$ решение уравнения для R имеет вид:
$R=\frac{1}{\sqrt{\pi r^3_0}}e^{-\frac{r}{r_0}}$ (8)
где $r_0$ - первый боровский радиус.
Интересно установить, на каком расстоянии от ядра вероятность нахождения электрона максимальна. Ее можно найти как максимум выражения $R^24\pi r^2$.
Расчет показывает, что наибольшей вероятности нахождения электрона соответствует расстояние от ядра, равное первому боровскому радиусу $r_0$.
При $n=2$ и $l=0$
$\Psi =R=N_2\left(\frac{r}{r_0}-2\right)e^{-\frac{r}{2r_0}}$ (9)
где $N_2$ - нормировочный множитель, выбираемый таким образом, чтобы соблюдалось равенство
Значение $\Psi $ здесь также не зависит от углов наклона и поворота При этом наибольшей вероятности нахождения электрона соответствует второй боровский радиус.
Очевидно, собственные функции электронов с $l=0$ ($s$-электронов) не зависят от угловых координат, а зависят только от радиуса. Следовательно, $s$-орбитали обладают шаровой симметрией (рис.1).

Рисунок 1.
При $n=2$ и $l=1$
$R=N_3re^{-\frac{r}{2r_0}}$ (10)
а для $\Theta $ возможен набор значений:

Рисунок 2.
Эти значения соответствуют значениям магнитного квантового числа $m_l = 0$ и $m_l = ±1$.
Здесь мы видим, что значения $\Theta $ и $\Psi $ не зависят от угла поворота $\varphi $, (т.к. по абсолютному значению $e^\pm i \varphi = 1$) т.е. $p$-орбитали обладают радиально-осевой симметрией. Перейдя к декартовым координатам и рассматривая линейные комбинации решений с тремя различными значениями $\Theta $, можно прийти к выводу, что орбитали с $m_l = 0$, $m_l = 1$ и $m_l = -1$ симметричны относительно осей координат $x$, $y$ и $z$. Иначе говоря, их оси симметрии вращения взаимно перпендикулярны. Соответствующие р-орбиталям электронные облака имеют вид объемных «восьмерок» или гантелей, расположенных взаимно перпендикулярно (рис.):
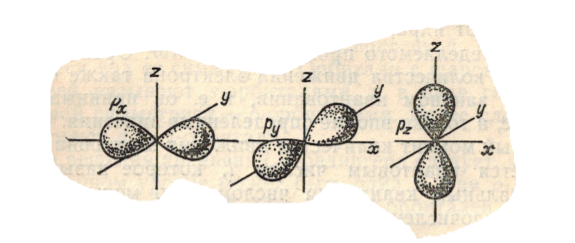
Рисунок 3.
Граничные поверхности $d$- орбиталей имеют форму розетки или сложной гантели с тороидом (рис.4). Таких орбиталей $5$, и каждая соответствует какому либо значению $m_l$ от $-2$ до $+2$.
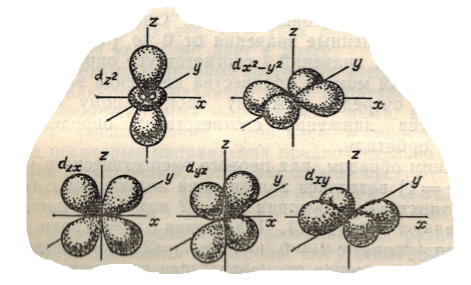
Рисунок 4.
Симметрия и форма $f$-орбиталей сложны для наглядного изображения форму. При этом те и другие также отличаются друг от друга не только по форме, но и по взаимному расположению в пространстве, что соответствует различным значениям магнитного квантового числа $m_l$.
Вообще, симметрия орбитали или, в упрощенном понимании - ее геометрическая форма, является важной характеристикой орбитали, характеризующей способность взаимодействовать с орбиталями других атомов, близких по энергии и симметрии, с образованием химических связей.












