
Атом водорода $(Н)$ - простейший атом, состоящий из ядра, содержащего 1 протон, и одного электрона, который движется в поле ядра. Простое строение атома водорода позволяет получить для него точное решение уравнения Шредингера.
Точное решение уравнения Шредингера возможно для частиц с одним электроном и любым значением заряда ядра. Такие объекты называют водородоподобными ионами. Вообще, ионами в химии называют частицы, состоящие из одного или нескольких атомов и имеющие отличный от нуля положительный или отрицательный электрический заряд, кратный по величине заряду электрона. Для многоэлектронных атомов решение уравнения Шредингера усложняется с ростом числа электронов и требует использования различных приближений.
При этом квантовый характер строения атома проявляется в том, что весь спектр частных решений уравнения Шредингера определяется перебором 4-х параметров - т.н. квантовых чисел, набор которых характеризует состояние электрона в атоме.
Главное квантовое число $n$ соответствует номеру энергетического уровня в модели атома Бора и определяет энергию электрона. Последняя тем больше, чем больше $n$.
Изучение атомных спектров показало, что отдельные спектральные линии не однородны, а состоят из более тонких близко расположенных линий. В этом случае уровень распадается на неравные, но близкие по энергии подуровни. Это связано с тем, что квантуется не только энергия электрона, но и его момент импульса. Его изменение определяется орбитальным квантовым числом $l$, которое может принимать значения от 1 до ($n-1$). Т.е. для уровня с $n=1$ возможен только один подуровень с $l=0$, для $n=2 - 2$ подуровня с $l=0$ и $l=1$, для $n=3 - 3$ подуровня с $l=0$, $l=1$, $l=2$ и т.п. В общем, число подуровней на одном уровне равно главному квантовому числу, соответствующему этому уровню.
Подуровни с $l=0, 1, 2, 3$ принято обозначать латинскими буквами $s-$, $p-$, $d-$, $f-$ и называть $s$-подуровнями, $p$-подуровнями, $d$-подуровнями, $f$-подуровнями соответственно, а находящиеся на них электроны - $s$-электронами, $p$-электронами, $d$-электронами, $f$-электронами соответственно.
Энергетические состояния электрона обозначают цифрой, соответствующей уровню и буквой, соответствующей подуровню. Например, запись $2s$-электрон означает, что электрон находится на s-подуровне второго уровня. Если на подуровне находится несколько электронов, то их количество указывается как верхний индекс («показатель степени») после буквенного обозначения подуровня. Например, если на $d$-подуровне 3-го уровня имеется 5 электронов, это будет записываться как $3d^5$.
Подуровни, в свою очередь, могут расщепляться еще более тонко. Это расщепление связано с неодинаковостью формы орбиталей различных электронов, их пространственного расположения и характером взаимодействия их магнитных полей и внешнего магнитного поля. Это расщепление характеризуется магнитным квантовым числом $m_l$. Для каждого значения $l$ $m_l$ принимает все целочисленные значения от $-l$ до $+l$. Т.е. если $l=0$, то $m_l$ принимает только одно значение, равное $0$. Следовательно, на каждом уровне может быть только одна $s$-орбиталь. Если $l=1$, то это значит, что $m_l$ может принимать одно из 3 значений: $-1$, $0$, $+1$. С учетом того, что $l$ может быть равным $1$ только при $n=2,3,4$ и т.п. это значит, что на каждом из уровней, начиная со второго, может быть по 3 $р$-орбитали. Если $l=2$, то $m_l$ принимает значения $-2$, $-1$, $0$, $+1$, $+2$, т.е. $d$-орбиталей на уровнях, начитая с 3-го ($n=3$) может быть $5$. Таким же образом можно показать, что на каждом уровне, начиная с 4-го ($n=4$), может быть $7$ $f$-орбиталей, для которых $m_l$ принимает значения $-3$, $-2$, $-1$, $0$, $+1$, $+2$, $+3$.
В одной орбитали может находиться не более двух электронов. Если в атомной орбитали находится только один электрон, как в атоме водорода, то такую орбиталь называют полузаполненной или полузаселенной. Если на теоретически возможной орбитали электронов нет, то ее называют вакантной. Полузаселенные и вакантные орбитали играют важнейшую роль при образовании химических связей.
В многоэлектронных атомах встречаются и орбитали с двумя электронами, которые являются полностью заселенными. При этом 2 электрона, находящиеся в одной орбитали, различаются по спину. Спин - квантово-механическое свойство электрона, которому трудно найти аналог в классической механике. Без учета волновых свойств электрона спин можно приближенно представить себе, сравнив электрон с вращающимся вокруг своей оси шаром. При этом спин будет характеризовать направление вращения, т.е. его знак будет меняться в зависимости от того, в какую сторону вращается электрон. Два электрона на одной орбитали обладают антипараллельными спинами, т.е. им соответствуют 2 противоположных значения спинового квантового числа, равные $+1/2$ и $-1/2$.
Атомную орбиталь удобно изображать в виде квадратной клетки, называемой квантовой ячейкой. Находящиеся на ней электроны обозначаются стрелками. Если орбиталь полностью заселена, стрелки направлены в противоположные стороны, что обозначает их антипараллельные спины.

Рисунок 1.
Таким образом, единственный электрон атома водорода в основном состоянии характеризуется следующим набором квантовых чисел:
$n=1$, $l=0$, $m_l=0$, $s=+1/2$
При возбуждении электрона главное квантовое число может принимать значение 2, 3, 4 и т.д. Все возможные электронные состояния, соответствующие значениям n от 1 до 4 приведены в табл.
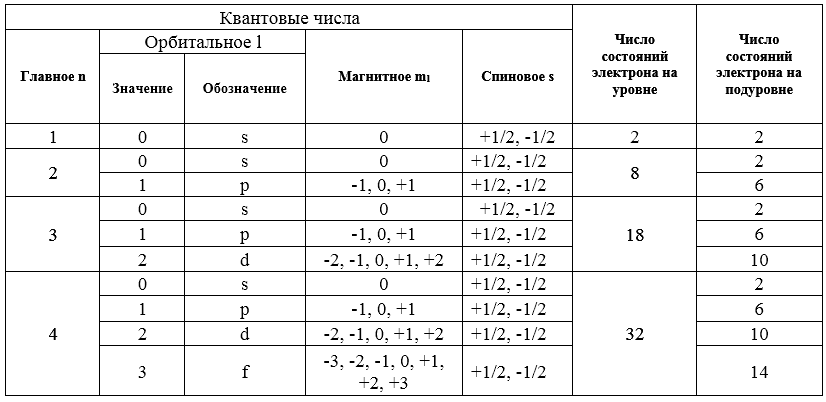
Рисунок 2.
Схема состояний электрона в атоме водорода для $n = от 1$ до $4$ изображена ниже:
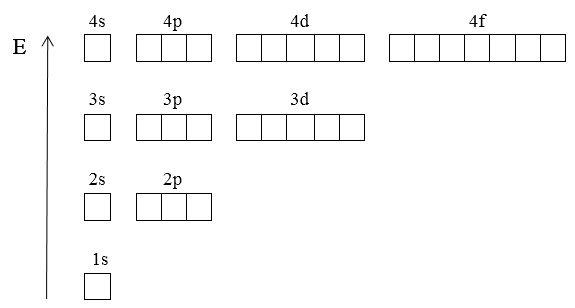
Рисунок 3.
На схеме показано, что в пределах одного и того же уровня $n$ подуровни $s$, $p$ и $d$ атома водорода вырождены, т.е. их энергии одинаковы. В невозбужденном состоянии электрон атома водорода или водородоподобного иона находится «в ячейке» $1s$, соответствующей самому низкому по энергии уровню.
Принцип, по которому количество подуровней, орбиталей и состояний электрона в атоме водорода может изменяться в зависимости от главного квантового числа n, может быть распространен и на многоэлектронные атомы. Однако ряд их особенностей, связанных с большим числом электронов и более «плотной упаковкой» электронных слоев создает ряд дополнительных особенностей, которые требуют отдельного рассмотрения.











