Введение
Состояние каждого электрона в атоме описывается волновой функцией, которая называется атомной орбиталью (или уровнем) и характеризуется тремя квантовыми числами. Соответствующие волновые функции выводятся из уравнения Шредингера и должны удовлетворять следующим требованиям: непрерывность, однозначность и конечность каждой волновой функции. При нарушении хотя бы одного из этих требований волновая функция оказывается непригодной для описания состояния электронов в атоме. Следовательно, дискретность энергетических состояний, в которых могут находиться электроны в атоме, является прямым следствием уравнения Шредингера. То же касается и трех квантовых чисел.
Главное квантовое число
Главное квантовое число может принимать любое целочисленное значение:
Но атомы известных в настоящее время элементов в стационарном состоянии (т.е. невозбужденные) не содержат электроны, для описания которых необходимы были бы атомные орбитали (уровни) с $n > 7$. Поэтому, в общем случае, реальным верхним пределом изменения главного квантового числа является значение $7$. Главное квантовое число характеризует энергию электрона на соответствующей орбитали. Или, проще говоря, степень удаленности данной орбитали от ядра атома (рис. 1). Чем меньше $n$, тем больше энергия связи электрона с ядром, т.е. тем большее, при прочих равных условиях, количество энергии требуется для удаления этого электрона из атома (эта энергия называется энергией ионизации).
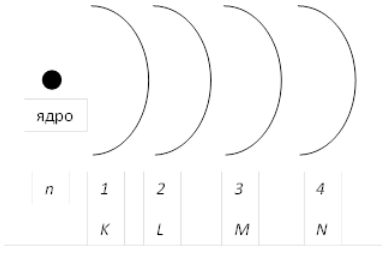
Рисунок 1. Схема раположений орбиталей атома
Забегая вперед, стоит сказать, что иногда для краткости записи электронной конфигурации атома вместо главного квантового числа используется буквенное обозначение соответствующих орбиталей (рис. 1): $K (n = 1)$, $L (n = 2)$, $M (n = 3)$, $N (n = 4)$, и так далее по алфавиту.
Орбитальное квантовое число
Орбитальное квантовое число $l$ может принимать значения от $0 до(n - 1)$:
Таким образом, $l$ для первых четырех значений главного квантового числа $n$ принимает следующие значения:

Рисунок 2.
Орбитальное квантовое число определяет форму соответствующего электронного облака (рис. 4). В записи электронной конфигурации атома оно обозначается по первым буквам английских наименований соответствующих спектральных линий $(sharp - s$, $principal - p$, $diffuse - d$, $fundamental - f$):

Рисунок 3.
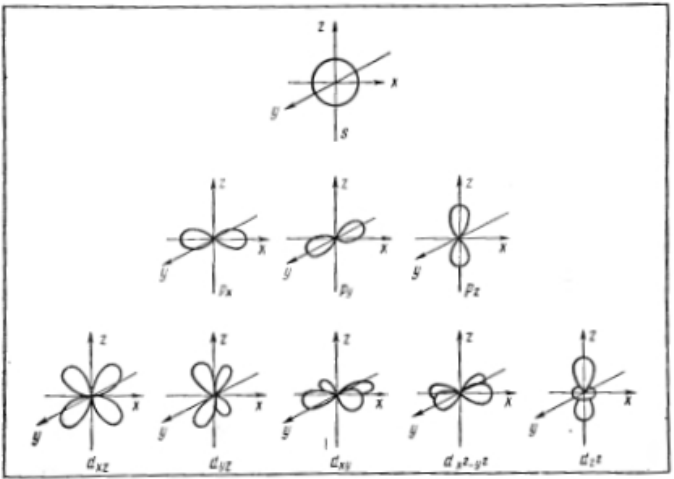
Рисунок 4. Формы электронных облаков атомных $s-$, $p-$, $d-$ орбиталей и их пространственное расположение
Таким образом, для каждого значения $n$ возможны строго определенные (по количеству и характеру) атомные орбитали (подуровни):
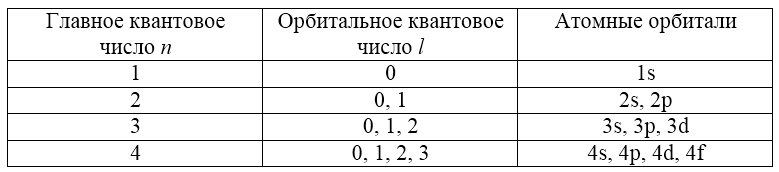
Рисунок 5.
Причем значения энергии электронов на соответствующих орбиталях таковы, что подуровень $4s$ расположен ближе к ядру, чем $3d$. Это правило пригодится при решении задач на составление электронных конфигураций атомов.
Магнитное квантовое число
Магнитное квантовое число m может принимать любые целочисленные значения от $+l$ до $-l$, включая $0$, и характеризует расположение соответствующей орбитали в пространстве атома:
Количество значений магнитного квантового числа определяется значением орбитального квантового числа $l$ и равно $(2l + 1)$:

Рисунок 6.

При заданных значениях $n$ и $l$ все возможные атомные орбитали независимо от значений m имеют одинаковую энергию, т.е. являются вырожденными. Кратность вырождения определяется числом атомных орбиталей с одинаковой энергией, т.е. числом значений m при заданном значении $l$. Таким образом, $s$-состояние электрона является вырожденным ($m = 0$), $p$-состояние - трехкратновырожденным ($m = 1$, $0$, $-1$), $d$- состояние - пятикратновырожденным, и.т.д.
Физический смысл магнитного квантового числа схематично представлен на рис. 7, где клетки - это, по сути, места, которые могут быть заняты электронами.
Спиновое квантовое число
Кроме всего прочего, электроны в атоме отличаются собственным моментом количества движения, который условно можно представить как вращение вокруг собственной оси. Это вращение характеризуется спиновым квантовым числом s, которое может иметь лишь два значения $+1/2$ и $-1/2$ (условно говоря, вращение по часовой стрелке и против часовой стрелки).
Примеры решения типовых задач
Записать электронную конфигурацию атома гелия в основном состоянии.
Решение. Главное квантовое число $n = 1$, орбитальное квантовое число $l = n - 1 = 0$, что соответствует s-состоянию. Таким образом, электронная конфигурация атома гелия $1s^2$, где индекс $2$ указывает на число электронов, занимающих орбиталь $1s$.
Записать электронную конфигурацию атома железа с порядковым номером $26$.
Решение. В соответствии с порядком заполнения атомных орбиталей имеем $1s^22s^22p^63s^23p^64s^23d^6$.












