Понятие вектора
Иногда, к примеру, в физике, для характеристики некоторых величин необходимо не только их числовое значение, но и направление (скорость, ускорение, сила...). Такие величины называются векторными величинами или коротко векторами. Напомним, что величины, не требующие направления, называются скалярными величинами.
Для введения понятия геометрического вектора будем использовать понятие отрезка. Введем следующее определение.
Граничные точки отрезка - это концы отрезка.
Отрезок может иметь два направления. Для обозначения направления будем называть одну граничную точку отрезка началом, а другую концом. Направление будет указываться от начала отрезка к его концу.
Вектором или направленным отрезком называется отрезок, для которого указано, какая из граничных точек считается началом, а какая концом данного отрезка.
Обозначение: $\overrightarrow{AB}$ - вектор $AB$ с началом в точке $A$ и концом в точке $B$.
Также вектор может обозначаться одной маленькой буквой: $\overrightarrow{a}.$
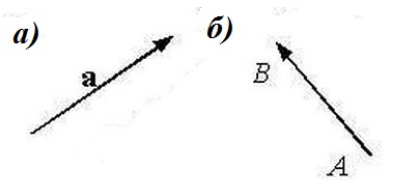
Рисунок 1. Примеры векторов: а) вектор $\overrightarrow{a}$; б) вектор $\overrightarrow{AB}$.
Введем еще несколько понятий, связанных с понятием вектора.
Нулевым вектором называется любая точка плоскости.
Обозначение: $\overrightarrow{0}$.
Длиной или модулем вектора $\overrightarrow{a}$ называется длина отрезка $a.$
Обозначение: $|\overrightarrow{a}|$
Отметим, что длина нулевого вектора равна нулю: $\left|\overrightarrow{0}\right|=0$.
Равенство векторов
Для введения определения равных векторов для начала нужно ввести несколько других понятий.
Ненулевые векторы называются сонаправленными, если они:
-
Коллинеарны.
-
Направлены в одну и туже сторону (рис. 3).
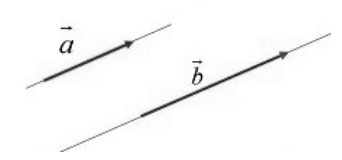
Рисунок 3. Сонаправленные векторы
Обозначение: $\overrightarrow{a}\uparrow \uparrow \overrightarrow{b}$
Ненулевые векторы называются противоположно направленными, если они:
-
Коллинеарны.
-
Направлены в разные стороны (рис. 4).
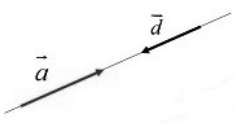
Рисунок 4. Противоположно направленные векторы
Обозначение: $\overrightarrow{a}\uparrow \downarrow \overrightarrow{d}$
Введем теперь непосредственно определение равных векторов.
Векторы называются равными, если:
-
Они являются сонаправленными;
-
Они имеют равные длины.
То есть, если $\overrightarrow{a}\uparrow \uparrow \overrightarrow{b}$ и $\left|\overrightarrow{a}\right|=|\overrightarrow{b}|$, то $\overrightarrow{a}=\overrightarrow{b}$ (рис. 5).

Рисунок 5. Равные векторы
Примеры задач на понятие вектора
Найти длину векторов, если одна клетка имеет площадь $1\ {см}^2$(рис. 6).
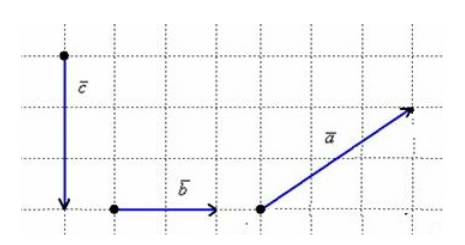
Рисунок 6.
Решение.
Так как клетка имеет площадь $1\ {см}^2$, то очевидно, что
\[\left|\overrightarrow{b}\right|=2\] \[\left|\overrightarrow{c}\right|=3\]Длину вектора $\overrightarrow{a}$ найдем с помощью теоремы Пифагора. Получим:
\[{|\overrightarrow{a}|}^2=3^2+2^2\] \[{|\overrightarrow{a}|}^2=9+4\] \[{|\overrightarrow{a}|}^2=13\] \[\left|\overrightarrow{a}\right|=\sqrt{13}\]Ответ: $\left|\overrightarrow{a}\right|=\sqrt{13}$, $\left|\overrightarrow{b}\right|=2$, $\left|\overrightarrow{c}\right|=3$.
Найти равные векторы (рис 7).
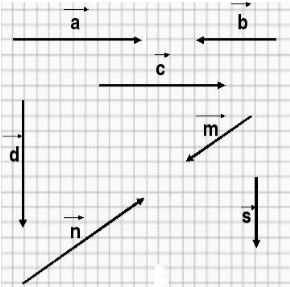
Рисунок 7.
Решение.
Используя определение 8, видим, что $\overrightarrow{a}\uparrow \uparrow \overrightarrow{c}$ и $\left|\overrightarrow{a}\right|=|\overrightarrow{c}|$, следовательно, $\overrightarrow{a}=\overrightarrow{c}$
Ответ: $\overrightarrow{a}=\overrightarrow{c}$.








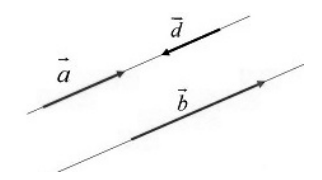 Коллинеарные векторы">
Коллинеарные векторы">


