Построение треугольников. Задачи на построение

Решение задач на построение состоит из четырех основных этапов:

• анализа;
• построения;
• доказательства;
• исследования.

Каждый этап является важным. Например, анализ и исследование задачи необходимы для рассмотрения случаев, когда задача будет иметь решение, а когда – нет.

Построение фигур проще выполнять с помощью транспортира и линейки с делениями, но в математике необходимо уметь выполнять построение, используя циркуль и линейку без делений.

Построение отрезка, равного заданному

Построить отрезок, равный заданному, можно за 3 действия. Каждое действие обозначено на рисунке соответствующими цифрами.

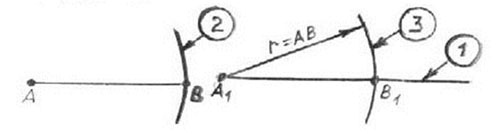
Пусть необходимо построить отрезок, который будет равен отрезку $АВ$. Для этого:

1. Отметим произвольно точку $А_1$ и проведем луч с началом в этой точке.
2. С помощью циркуля измерим заданный отрезок $АВ$.
3. Проведем часть окружности с радиусом, равным отрезку $АВ$, и центром в точке $А_1$. В точке пересечения окружности и построенного луча получим точку $В_1$.

Таким образом, построенный отрезок $А_1 В_1$ будет равен заданному отрезку $АВ$.

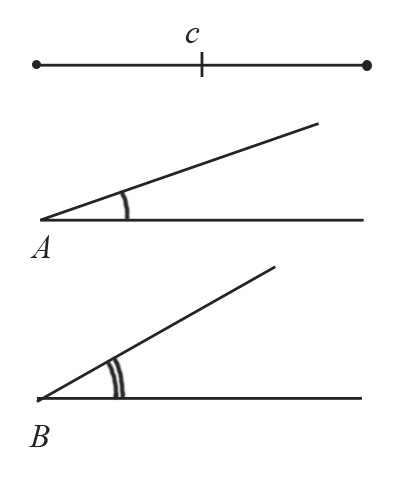
Построение угла, равного заданному

Построить угол, равный заданному, можно за $5$ действий. Каждое действие обозначено на рисунке соответствующими цифрами.

Пусть необходимо построить угол, который будет равен углу $А$.

Для этого:

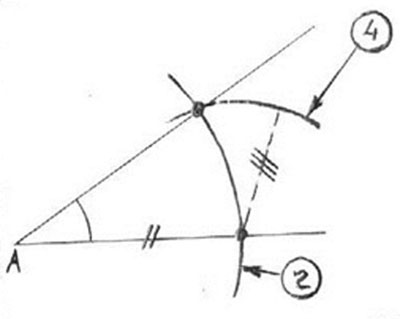
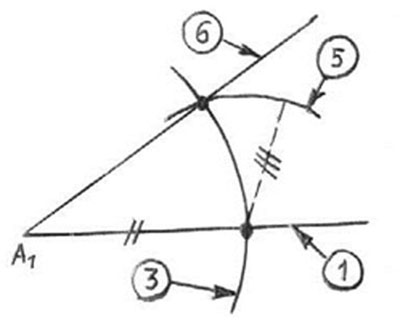
1. Отметим произвольную точку $А_1$ и проведем из нее луч $А_1$.
2. Циркулем с произвольным радиусом проведем часть окружности с центром в точке $А$ до пересечения обеих сторон заданного угла $А$.
3. С тем же радиусом проведем часть окружности с центром в точке $А_1$ до пересечения с лучом $А_1$.
4. Из точек пересечения проведем окружности с одинаковым радиусом.
5. Проведем прямую из точки $А_1$ через вторую точку пересечения.

Построение треугольника по двум сторонам и углу между ними

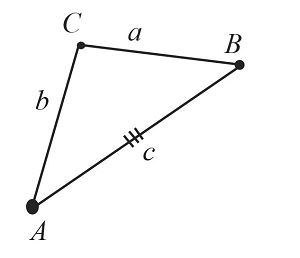
Пусть даны два отрезка $b$ и $с$ и угол $А$:

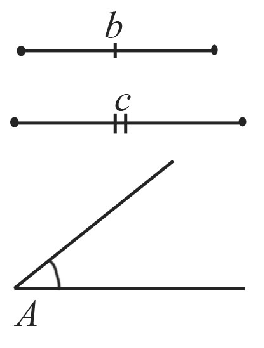
Необходимо построить треугольник с заданными двумя сторонами и углом между ними:

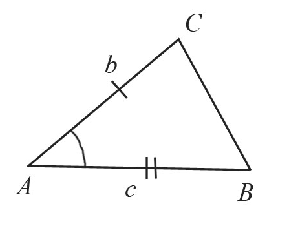
Построение выполняется в 4 этапа, каждый из которых показан на рисунках:

1. Построим угол $А$, который равен заданному углу по схеме, которая рассматривалась выше.

   

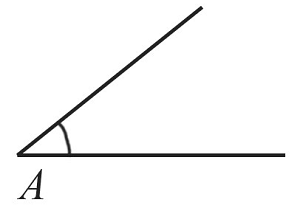
2. С помощью циркуля замеряем отрезок $b$ и отложим от точки $А$ такой же отрезок на одной из сторон построенного угла. Получим точку $С$.

   

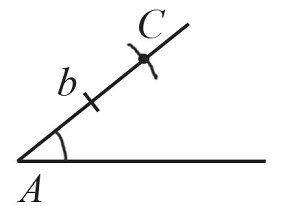
3. Циркулем замеряем отрезок $с$ и отложим от точки $А$ такой же отрезок на второй стороне построенного угла. Получим точку $В$.

   

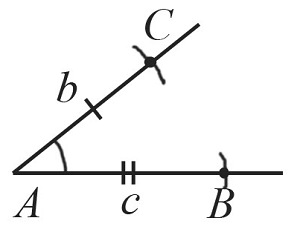
4. С помощью линейки соединим точки $В$ и $С$.

   

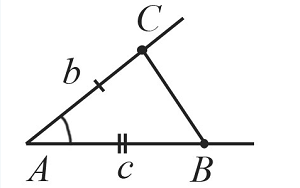
Таким образом, получили треугольник $АВС$, построенный по двум сторонам и углу между ними.

Для облегчения построения полезно схематически изобразить будущий треугольник со всеми необходимыми элементами. Так будет наглядней видно, что после чего нужно строить.

Построение треугольника по стороне и прилегающим к ней углам

Пусть даны два угла $А$ и $В$ и отрезок $с$:

Необходимо построить треугольник с заданными двумя углами и стороной, к которой они прилегают:

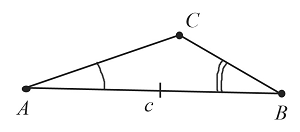
Построение выполняется в $3$ этапа, каждый из которых показан на рисунках:

1. Начертим произвольный отрезок $АВ$, который равен заданному отрезку $c$.

   

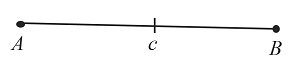
2. Построим угол $А$, который равен заданному, как показано выше.

   

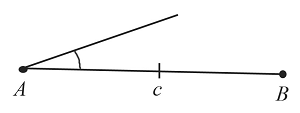
3. Построим угол $В$, который равен заданному.

   

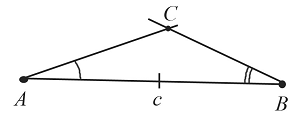
Точка пересечения двух сторон построенных углов $А$ и $В$ является вершиной треугольника $С$.

Таким образом, получили треугольник $АВС$, построенный по стороне и двум углам.

Построение треугольника по трем сторонам

Пусть даны $3$ отрезка $а$, $b$ и $с$.

Необходимо построить треугольник по трем заданным сторонам.

1. Построим отрезок $АВ$, который равен заданному отрезку $c$.

   

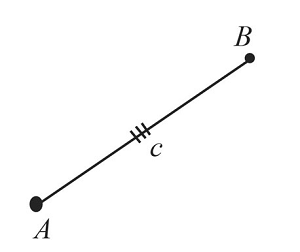
2. Из точки $А$ проведем часть окружности с радиусом, равным заданному отрезку $b$.

   

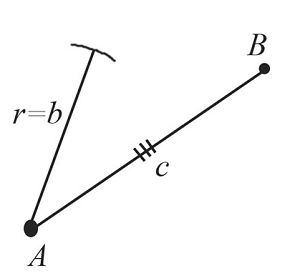
3. Из точки $В$ проведем часть окружности с радиусом, равным заданному отрезку $a$. Пересечением обеих окружностей является точка $С$.

   

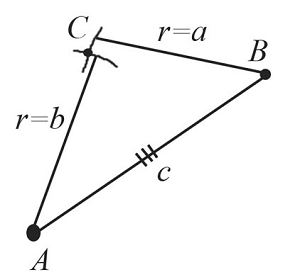
Таким образом, получили построенный треугольник $АВС$ по трем заданным сторонам.