Для понятия проекции вектора на ось или какой-либо другой вектор существуют понятия ее геометрической проекции и числовой (или алгебраической) проекции. Результатом геометрической проекции будет вектор, а результатом алгебраической – неотрицательное действительное число. Но перед тем, как перейти к этим понятиям вспомним необходимую информацию.
Предварительные сведения
Основное понятие – непосредственно понятие вектора. Для того, чтобы ввести определение геометрического вектора вспомним, что такое отрезок. Введем следующее определение.
Отрезком будем называть часть прямой, которая имеет две границы в виде точек.
Отрезок может иметь 2 направления. Для обозначения направления будем называть одну из границ отрезка его началом, а другую границу - его концом. Направление указывается от его начала к концу отрезка.
Вектором или направленным отрезком будем называть такой отрезок, для которого известно, какая из границ отрезка считается началом, а какая его концом.
Обозначение: Двумя буквами: $\overline{AB}$ – (где $A$ его начало, а $B$ – его конец).
Одной маленькой буквой: $\overline{a}$ (рис. 1).
Введем еще несколько понятий, связанных с понятием вектора.
Два ненулевых вектора будем называть коллинеарными, если они лежат на одной и той же прямой или на прямых, параллельных друг другу (рис.2).
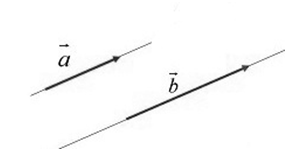
Два ненулевых вектора будем называть сонаправленными, если они удовлетворяют двум условиям:
- Эти векторы коллинеарны.
- Если они будут направлены в одну сторону (рис. 3).
Обозначение: $\overline{a}↑↑\overline{b}$
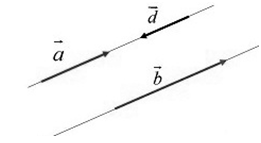
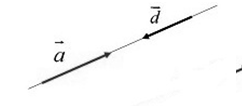
Два ненулевых вектора будем называть противоположно направленными, если они удовлетворяют двум условиям:
- Эти векторы коллинеарны.
- Если они направлены в разные стороны (рис. 4).
Обозначение: $\overline{a}↑↓\overline{d}$
Длиной вектора $\overline{a}$ будем называть длину отрезка $a$.
Обозначение: $|\overline{a}|$
Перейдем к определению равенства двух векторов
Два вектора будем называть равными, если они удовлетворяют двух условиям:
- Они сонаправлены;
- Их длины равны (рис. 5).
Геометрическая проекция
Как мы уже сказали ранее, результатом геометрической проекции будет вектор.
Геометрической проекцией вектора $\overline{AB}$ на ось будем называть такой вектор, который получается следующим образом: Точка начала вектора $A$ проецируется на данную ось. Получаем точку $A'$ - начало искомого вектора. Точка конца вектора $B$ проецируется на данную ось. Получаем точку $B'$ - конец искомого вектора. Вектор $\overline{A'B'}$ и будет искомым вектором.
Рассмотрим задачу:
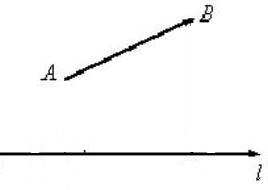
Постройте геометрическую проекцию $\overline{AB}$ на ось $l$, изображенные на рисунке 6.
Решение.
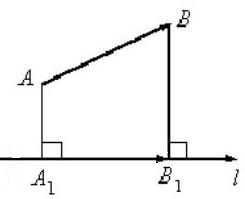
Проведем из точки $A$ перпендикуляр к оси $l$, получим на ней точку $A'$. Далее проведем из точки $B$ перпендикуляр к оси $l$, получим на ней точку $B'$ (рис. 7).
Полученный на оси $l$ вектор $\overline{A'B'}$ и будет искомой геометрической проекцией.
Заметим, что если угол между вектором и осью острый, то проекция сонаправлена с осью, а если тупой, то проекция противоположно направлена с осью.
Числовая проекция
Как мы уже знаем, результатом алгебраической проекции будет неотрицательное действительное число.
Числовой (алгебраической) проекцией на ось будем называть неотрицательное число, равное длине вектора геометрической проекции.
Рассмотрим это понятие на примере задачи:
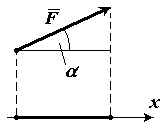
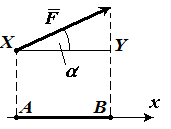
Найти числовую проекцию вектора $\overline{F} на сонаправленную ему ось $x$, если угол между ними равняется $α$ (рис. 8). (рис. 8).
Решение.
Введем на рисунке следующие обозначения:
Видим, что длина вектора геометрической проекции, равняется длине $XY$. Из определения косинуса получим, что
$XY=|\overline{F}|cosα$
где $|\overline{F}|$ - длина вектора $\overline{F}$. Это и будет искомая алгебраическая проекция на ось.
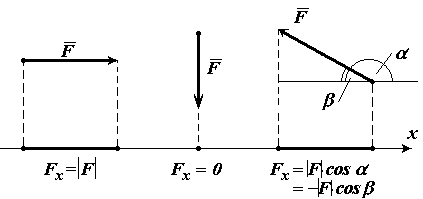
Другие случаи можете видеть на рисунке 9.