Вибратор Герца
Простейший пример излучающей электрической системы - вибратор Герца. Это электрический диполь, момент которого переменен во времени. На практике основную часть вибратора Герца составляют два металлических шарика, которые соединяются проводником (металлическим стержнем с небольшим искровым промежутком посередине). Шарам сообщают одинаковые по модулю и противоположные по знаку заряды и предоставляют систему самой себе. В системе происходит колебательный процесс, который состоит в перезарядке шариков. Колебания являются затухающими. Если шарики имеют маленькое сопротивление, потери за счет излучения небольшие (за один период), то затуханием колебаний можно пренебречь в течение нескольких периодов. В таком случае, на расстояниях от вибратора много больших, чем расстояние между шариками ($l$), систему можно считать диполем с переменным во времени моментом. Сам вибратор часто называют диполем Герца.
Подобную конструкцию использовал Герц, первый в опытах получивший электромагнитные волны. Электроемкость вибратора, в большей степени определяется электроемкостью шаров, а индуктивность - индуктивностью стержня. Возбудителем электромагнитных колебаний в вибраторе является индукционная катушка. Если переменное напряжение во вторичной обмотке катушки достигает величины пробивного напряжения, то в искровом промежутке возникает искра, половинки вибратора замыкаются. Возникают высокочастотные колебания, которые сопровождаются излучением электромагнитных волн. Частота колебаний в экспериментах Герца достигалась значений порядка ${10}^8Гц$. Для того чтобы регистрировать электромагнитные волны, Герц применял резонатор в виде проволочного кольца с искровым промежутком. В кольце под воздействием поля электромагнитной волны появлялись вынужденные электромагнитные колебания. Собственные частоты вибратора и кольца были одинаковы, возникал резонанс. Амплитуда вынужденных колебаний в резонаторе достигала существенных значений, колебания обнаруживались по проскакиванию искры в искровом промежутке.
Если размеры шаров уменьшить, уменьшается электроемкость шаров, увеличивается частота электромагнитных колебаний. Так Герцу удалось получить коротковолновое электромагнитное излучение с длиной волны $\lambda \approx 60\ см.$
Позднее П.Н. Лебедев сделал вибратор, который состоял из двух кусков платиновой проволоки длиной по $1,5 мм$ каждый, и получил электромагнитные волны длиной $\lambda \approx 6\ мм.$
А.А. Глаголева - Аркадьева применила массовый излучатель, в котором миниатюрными вибраторами стали металлические опилки в вязком масле, чем добилась излучения с $\lambda \approx 82мкм.$
Скалярный и векторный потенциалы электромагнитного диполя
Скалярный потенциал диполя ($\varphi (r,t)$), переменного во времени можно определить как:
где считаем, что диполь локализован в вакууме ($\varepsilon =1,\ \mu =1$). При расчете $\varphi \left(r,t\right)$, обычно начало координат помещают в области распределения заряда, при этом несущественно, где расположено начало области распределения заряда, так как размеры диполя считают малыми в сравнении с расстояниями до точек рассмотрения поля. $\xi \ $- радиус-вектор элемента объема $dV_{\xi }$, $r'$- расстояние между элементом объема $dV_{\xi }$ и точкой наблюдения (рис.1).
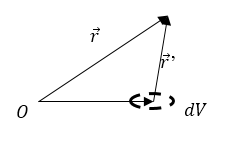
Рисунок 1.
На больших расстояниях от диполя ($\frac{\xi }{r}\ll 1$) потенциал диполя можно рассчитать как:
где $\overrightarrow{p}\left(t-\frac{r}{c}\right)=\int{\xi \rho \left(t-\frac{r}{c}\right)}dV_{\xi }$- момент диполя.
Векторный потенциал, изменяющийся со временем, определяется как:
Поле вибратора в зоне волны
Если расстояние $r$ до точек волновой поверхности удовлетворяет условию: $\frac{1}{r}\ll \frac{\omega }{c}$, момент диполя ($\overrightarrow{p}$) изменяется по гармоническому закону:
напряженность и индукция электромагнитного поля в волновой зоне вибратора имеют вид:
Система уравнений (5) показывает, что в волновой зоне электрический и магнитный векторы перпендикулярны друг другу и радиус - вектору $\overrightarrow{r}.$ При этом волна обладает сферической симметрией. Так как $E_{\theta }=cB_{\alpha }$, небольшие участки поверхности сферической волны можно принять как плоские электромагнитные волны.
Излучение электромагнитных волн
Процесс возникновения электромагнитной волны электрической системой называют излучением электромагнитных волн. Система при этом носит название - излучающей системы. Электромагнитное поле при этом является полем излучения.
Система, в которой имеется переменный электрический ток, создает переменное электромагнитное поле, и, значит, излучает электромагнитные волны. В том случае, если размеры системы малы по сравнению с длиной волны ($\lambda $), то излучение мало. При данных условиях ток в системе можно считать квазистационарным. Электромагнитные поля, которые генерируются отдельными участками системы, имеющими противоположные направления и равные токи, ослабляют друг друга. Следовательно, суммарное переменное электромагнитное поле быстро ослабевает, если расстояние от системы увеличивается, то есть данная система почти не излучает электромагнитных волн.
Для генерирования электромагнитных волн можно использовать ламповые генераторы, которые позволяют получать электрические колебания правильной синусоидальной формы и почти любой мощности. Для получения колебаний в вибраторе можно между его половинами $ВВ$ (рис.2) включить несколько витков связи, расположив их около катушки индуктивности $K$ и дампового генератора $Г$ (магнитная связь). Для усиления колебаний в вибраторе используют резонанс, делая частоту генератора равной собственной частоте основного колебания вибратора. Для выявления наличия колебаний в приемном вибраторе используют небольшую лампу или детектор.
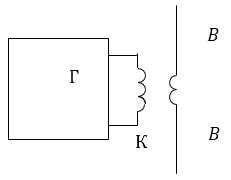
Рисунок 2.
Опыты Герца подтвердили свойства электромагнитных волн, которые предсказал Максвелл. Так Герц, например, показал, что электромагнитные волны являются поперечными. Как и световые волны, электромагнитные волны отражаются о поверхности раздела двух диэлектриков, преломляются при переходе через эту поверхность, отражаются от поверхности металла.
Чуть позже опытов Герца электромагнитные волны стали использовать для реализации беспроводной связи (радиосвязи). Первый радиоприемник, который регистрировал электромагнитное излучение грозовых разрядов, создал А.С. Попов. Кроме радиотелеграфии при помощи электромагнитных волн осуществляется передача речи и музыки (радиовещание), изображения (телевидение), разработаны методы радиолокации. Электромагнитное излучение применяется в самых разных радиотехнических устройствах.
Задание: Объясните, почему являются непригодными для создания электромагнитных волн колебательные контуры, состоящие из конденсатора и катушки индуктивности (закрытые контуры). А для передачи высокочастотных токов используют коаксиальные кабели?
Решение:
Колебательный контур, который состоит из конденсатора и катушки индуктивности, почти не излучает электромагнитных волн, так как переменное электромагнитное поле его локализовано только в пространстве между обкладками конденсатора и внутри соленоида. В окружающем пространстве электромагнитное поле практически равно нулю.
Коаксиальный кабель состоит из центрального провода, который идет по оси цилиндрического проводника. Он отделяется слоем диэлектрика от проводника - цилиндра. Переменное электромагнитное поле коаксиального кабеля полностью находится внутри диэлектрика. Так как вне кабеля поля нет, то нет потерь на излучение.
Задание: Чему равна средняя за период мощность излучения вибратора?
Решение:
В качестве основы для решения задачи используем определение потока электромагнитной энергии, который через поверхность $S$ сферы имеющей радиус $r$ равен:
\[P=\int\limits_S{\overrightarrow{E}\times \overrightarrow{H}d\overrightarrow{S}=\int\limits_S{E_{\theta }H_{\alpha }dS}=\frac{1}{16{\pi }^2{\varepsilon }_0}}\frac{{\omega }^4{p_0}^2}{c^3}{cos}^2\omega \left(t-\frac{r}{c}\right)\int\limits^{\pi }_0{{sin}^3\theta d\theta \int\limits^{2\pi }_0{d\alpha =\frac{1}{6\pi {\varepsilon }_0}}}\frac{{\omega }^4{p_0}^2}{c^3}{cos}^2\omega \left(t-\frac{r}{c}\right)\left(2.1\right).\]В выражении (2.1) мы получили мощность потока, то есть энергию излучения вибратора за $1 с$. Средняя мощность излучения вибратора за период равна:
\[\left\langle P\right\rangle =\frac{1}{T}\int\limits^T_0{Pdt}=\frac{1}{12\pi {\varepsilon }_0}\frac{{\omega }^4{p_0}^2}{c^3}.\]Ответ: $\left\langle P\right\rangle =\frac{1}{T}\int\limits^T_0{Pdt}=\frac{1}{12\pi {\varepsilon }_0}\frac{{\omega }^4{p_0}^2}{c^3}.$












