Состояние равновесия системы
Пусть система тел имеет постоянную температуру, внешние силы работы не совершают (объем системы не изменяется). При этом могут происходить процессы внутри системы. Если будет системой достигнуто состояние, при котором свободная энергия системы минимальна, то дальнейшие изменения в системе невозможны. Это состояние называют состоянием равновесия системы. Другими словами, в состоянии равновесия приращение свободной энергии (энергии Гельмгольца), при переходе из него в бесконечно близкое состояние, равно нулю. Подобным образом выражается условие равновесия с помощью энергии Гиббса. В этом случае постоянными должны быть температура и внешние силы (например, давление). В состоянии равновесия термодинамический потенциал должен иметь минимум.
Допустим, что некоторое количество компоненты 1 превращается из одной фазы в другую при постоянном удельном объеме $v$. Условие равновесия системы в отношении удельной свободной энергии ($f$), если некоторое бесконечно малое количество вещества ($\nu $) первой компоненты превратится из первой фазы во вторую, то $f^1$ получит приращение $-\frac{\partial f^1}{\partial {m_1}^1}\nu ,$ а $f^2-$ получит приращение $\frac{\partial f^2}{\partial {m_1}^2}\nu .\ $ Из условия $\sum{\delta f^k=0\ }$ следует, что уравнение равновесия относительно удельной свободной энергии будет иметь вид:
где массу i -- ой компоненты в k -- той фазе обозначили как $m^k_i$. Уравнение (1) можно считать условием равновесия между первыми двумя фазами по отношению к первой компоненте.
Три фазы компоненты
Пусть одна компонента вещества системы содержится в трех фазах. Составим уравнения равновесия для компоненты 1 в первой и третьей фазах, получим:
Уравнение равновесия для этой же компоненты во второй и третьей фазах:
Если первая и вторая фазы, находятся в равновесии для какой то компоненты с третьей фазой, то первая фаза будет находиться в равновесии и со второй.
Допустим, что в системе находится вещество в трех состояниях: твердом, жидком и газообразном. Для жидкости и газа уравнение состояния мы можем записать как ($\varphi -удельный\ термодинамический\ потенциал$):
\[{\varphi }_1={\varphi }_3\left(4\right).\]Для твердой и газообразной фаз, получим следующее:
\[{\varphi }_2={\varphi }_3\left(5\right).\]Для твердой и жидкой фаз, соответственно имеем:
\[{\varphi }_1={\varphi }_2\left(6\right).\]Если заданы ${\varphi }_1,{\varphi }_2,{\varphi }_3$ в виде функций от давления и температуры, то можно построить три кривые равновесия, по одной для каждой пары фаз. Пусть максимальное давление газа над жидкостью и над твердым телом одинаково, (так подобрана температура), тогда мы получим равновесие и между твердой и жидкой фазами. (Если ${\varphi }_1={\varphi }_3,\ ц_2=ц_3\to {\varphi }_1={\varphi }_2$). Точка пересечения этих трёх кривых -- тройная точка (рис.1).
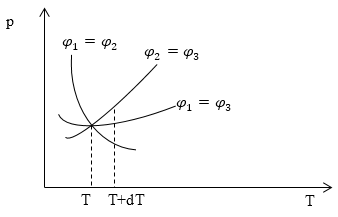
Рис. 1
Задание: Показать, что уравнение равновесия, записанное с помощью удельного термодинамического потенциала для системы при постоянном давлении равнозначно уравнению равновесия, которое записано с помощью удельной свободной энергии.
Решение:
Рассмотрим удельный термодинамический потенциал $\varphi $ как функцию $\varphi (p,T,\ m_1,m_2,m_3)$. $m_1,m_2,m_3$- массы первой, второй и третьей компоненты системы. Допустим, что бесконечно малое количество компоненты перешло из одной фазы в другую при $p=const$, $T=const$. Запишем уравнение равновесия между первой и второй фазами для удельного термодинамического потенциала:
\[{\left(\frac{\partial {\varphi }^1}{\partial {m_1}^1}\right)}_p={\left(\frac{\partial \varphi }{\partial {m_1}^2}\right)}_p\left(1.1\right).\]Уравнение (1.1) равносильно уравнению, которое определяет состояние равновесия для свободной энергии. Значок p внизу у правой скобки означает, что давление в системе постоянно. Возьмем частную производную от удельной свободной энергии по массе при постоянном давлении ${\left(\frac{\partial f}{\partial m}\right)}_p$. Мы можем записать следующее:
\[{\left(\frac{\partial f}{\partial m}\right)}_p={\left(\frac{\partial f}{\partial m}\right)}_V+{\left(\frac{\partial f}{\partial V}\right)}_m{\left(\frac{\partial v}{\partial m}\right)}_p\left(1.2\right),\]где
\[{\left(\frac{\partial f}{\partial V}\right)}_m=-p\left(1.3\right).\]Следовательно, выражение (1.2) преобразуется к виду:
\[{\left(\frac{\partial f}{\partial m}\right)}_p={\left(\frac{\partial f}{\partial m}\right)}_V-p{\left(\frac{\partial v}{\partial m}\right)}_p\left(1.4\right).\]Однако мы знаем, что удельная свободная энергия Гельмгольца и термодинамический потенциал Гиббса связаны соотношением:
\[\varphi =f+pv\ \left(1.5\right).\]Поэтому мы запишем:
\[{\left(\frac{\partial \varphi }{\partial m}\right)}_p={\left(\frac{\partial f}{\partial m}\right)}_V+p{\left(\frac{\partial v}{\partial m}\right)}_p\left(1.6\right).\]Из (1.6) вытекает равенство:
\[{\left(\frac{\partial f}{\partial m}\right)}_V={\left(\frac{\partial \varphi}{\partial m}\right)}_p\left(1.7\right).\]Таким образом, мы убедились, что условия равновесия, представленные через удельную свободную энергию Гельмгольца и через удельный термодинамический потенциал Гиббса эквивалентны, но используются при разных условиях. Свободная энергия при постоянном объёме, а термодинамический потенциал при постоянном давлении. Температура постоянна в обоих случаях.
Задание: Система из воды, льда и пара находится в состоянии термодинамического равновесия. Заданы удельные термодинамические потенциалы системы ${\varphi }_1,{\varphi }_2,{\varphi }_3$ в виде функций от давления и температуры, для газообразной, жидкой и твердой фаз. На рис. 1 построены три кривые равновесия, по одной для каждой пары фаз для воды пара и льда. Равновесие, каких фаз отображает кривая ${\varphi }_1={\varphi }_3$?
Решение:
Возьмем абсциссу вблизи от тройной точки (T- температура тройной точки) определим для какой кривой ордината наибольшая. Выбранной точкой на рис. 1 является точка $(T+dT).$ Приращению $dT$ соответствуют три разных приращения ординаты (давления). Обозначим их ${\left(dp\right)}_{12},\ {\left(dp\right)}_{23},\ {\left(dp\right)}_{31}.\ $При переходе от T к $T+dT$ вдоль кривой ${\varphi }_1={\varphi }_2$ получим:
\[\frac{\partial {\varphi }_1}{\partial T}dT+\frac{\partial {\varphi }_1}{\partial p}{\left(dp\right)}_{12}=\frac{\partial {\varphi }_2}{\partial T}dT+\frac{\partial {\varphi }_2}{\partial p}{\left(dp\right)}_{12}\ \left(2.1\right).\]или
\[(\frac{\partial {\varphi }_1}{\partial T}-\frac{\partial {\varphi }_2}{\partial T})dT+(v_1-v_2){\left(dp\right)}_{12}=0\ \left(2.2\right).\]По аналогии запишем для двух других кривых:
\[(\frac{\partial {\varphi }_2}{\partial T}-\frac{\partial {\varphi }_3}{\partial T})dT+(v_2-v_3){\left(dp\right)}_{23}=0\ \left(2.3\right).\]и
\[(\frac{\partial {\varphi }_3}{\partial T}-\frac{\partial {\varphi }_1}{\partial T})dT+(v_3-v_1){\left(dp\right)}_{31}=0\ \left(2.4\right).\]Сложим уравнения (2.2), (2.3), (2.4), получим:
\[\left(v_1-v_2\right){\left(dp\right)}_{12}+\left(v_2-v_3\right){\left(dp\right)}_{23}+(v_3-v_1){\left(dp\right)}_{31}=0\ \left(2.5\right).\]Для графика на рис. 1 ординатами, которые соответствуют температуре $T+dT$ будут давления: $p_{12},p_{23},p_{31}$.
Произведем замену:
\[v_2-v_3={(v}_2-v_1)+(v_1-v_3)\ (2.6),\]получим:
\[\frac{(p_{12}-p_{23})}{(p_{31}-p_{23})}=\frac{(v_1-v_3)}{(v_1-v_2)}\ \left(2.7\right).\]Разности давлений относятся между собой как разности удельных объемов. Можно сделать вывод о том, что кривая ${\varphi }_1={\varphi }_3$ относится к равновесию фаз с наибольшей разностью удельных объемов. Если диаграмма построена для воды, то такими фазами будут жидкость и газ.
Ответ: Кривая ${\varphi }_1={\varphi }_3$ относится к равновесию воды и водяного пара.











