Что такое термодинамика
Термодинамика -- важнейшая часть физики. Ее выводы используются в гиро- и аэродинамике, оптике, физической химии многих других науках и прикладных разработках.
Возникла термодинамика в начале XIX века. В то время начала свое развитие теплотехника. Термодинамика стала ее теоретической основой. Ее целью в то время было изучение закономерностей, которые определяют процессы превращения тепла в механическую работу с помощью тепловых двигателей и поиск условий, при которых максимальна эффективность таких превращений. Основы термодинамики заложил в своих работах Саади Карно, французский инженер и физик, который и исследовал тепловые двигатели. Тогда еще теплота рассматривалась как некоторое вещество -- теплород, которое не имеет массы и не может быть создано или уничтожено. Впоследствии термодинамика вышла за границы узкой технической задачи. Основным содержанием современной термодинамики стало изучение законов тепловой формы движения материи и связанных с этим явлений.
Какие процессы изучает термодинамика
Термодинамика изучает макроскопические процессы, которые происходят в телах, системах тел. Эта наука не использует специальных гипотез и представлений о строении вещества. Не задает вопросы о природе теплоты. Выводы термодинамики основаны на общих принципах (началах), которые получены обобщением эмпирических данных.
Термодинамика изучает только термодинамически равновесные состояния систем или очень медленные процессы, которые могут быть представлены совокупностью равновесных. Эта наука также изучает законы перехода от одного равновесного состояния к другому.
Выводы термодинамики весьма общие, так как получают их без использования упрощенных моделей. Термодинамика многие уравнения берет из опыта, или молекулярно -- кинетической теории. Но здесь необходимо отметить, что практика показала, что аксиомы термодинамики имеют границы применимости. Так классическая термодинамика плохо применима в системах с малыми размерами, так как не рассматривает флуктуации состояния, которые в микромире имеют существенное значение.
Итак, основную идею термодинамики определим так:
Макроскопические системы состоят из большого количества частиц. Состояния системы характеризуются вполне конкретными параметрами. Каждая система подчиняется закону сохранения энергии.
В термодинамике закон сохранения энергии формулируется как начала термодинамики. Поведение макросистемы описывается исходя из начал термодинамики. В термодинамике сформулированы три начала. Первое начало -- следствие закона сохранения энергии:
где $\delta Q$- элемент тепла (или бесконечно малое количество) подводимое к термодинамической системе. Изучение движение и превращений этой формы энергии является предметом термодинамики, $dU$- изменение внутренней энергии системы, $\delta A$ -- элементарная работа. Бесконечно малые величины здесь обозначены разными символами (d и $\delta $), это сделано намерено. С целью подчеркнуть, что свойства этих малых величин различны. Первое начало термодинамики не дает понятия о направлении прохождения процесса. Поэтому необходимо второе начало. Именно оно характеризует направление процессов в термодинамике. Существую несколько формулировок второго начала термодинамики. По форме они отличаются, но по смыслу он эквивалентны. Приведем одну из формулировок, ее дал Томпсон (лорд Кельвин):
«Невозможен круговой процесс, единственным результатом которого было бы производство работы за счет уменьшения внутренней энергии теплового резервуара».
Третье накладывает ограничение на процессы. Его сформулируем:
«Абсолютный нуль недостижим посредством конечного числа операций».
Математическим аппаратом термодинамики является теория дифференциальных форм и уравнения в частных производных.
Задание: Идеальный одноатомный газ совершает циклический процесс (рис.1).
Определите КПД цикла, если известны $V_1,\ V_2,$ $p_1,\ p_2$.
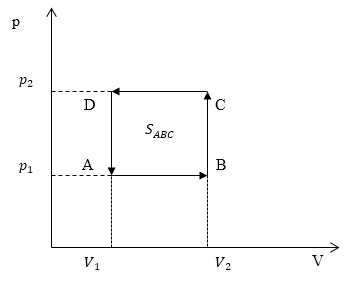
Рис. 1
Решение:
Кпд ($\eta $) цикла в данном случае удобно определить как:
\[\eta =\frac{A}{Q^+}\left(1.1\right),\]где A -- работа газа в круговом процессе, $Q^+$- количество теплоты, подведенное газу от нагревателя.
Круговой процесс (цикл), который изображен на рис.1, состоит из четырех последовательных процессов. Определим, в каких процессах тепло подводится. Очевидно, что это процессы AB и BC.
Процесс AB -- изобарный. Запишем первое начало термодинамики и найдем количество теплоты, пущенное газом в этом процессе.
\[\triangle Q=\triangle U+A\ \left(1.2\right).\]Работа в изобарном процессе может быть найдена как:
\[A=p\triangle V\ \left(1.3\right).\]Следовательно, для процесса AB мы получим:
\[A_{AB}=p_1\left(V_2-V_1\right)\left(1.4\right).\]Изменение внутренней энергии газа в процессе AB, имеет формулу:
\[\triangle U_{AB}=\frac{i}{2}\nu R\left(T_2-T_1\right)\left(1.5\right).\]Для того, чтобы найти $\left(T_2-T_1\right)$, используем уравнение Менделеева - Клайперона для идеального газа. Запишем его для двух состояний (точек A и B):
\[p_1V_1=\nu RT_1\left(1.6\right).\] \[p_1V_2=\nu RT_2\left(1.7\right).\]Найдем разность (1.7) и (1.6), получим:
\[p_1\left(V_2-V_1\right)=\nu R{(T}_2-T_1)\ (1.8).\]Подставим (1.8) в (1.5), получим:
\[\triangle U_{AB}=\frac{i}{2}p_1\left(V_2-V_1\right)\left(1.9\right).\]Следовательно, количество теплоты, полученное газом в процессе AB равно:
\[\triangle Q_{AB}=p_1\left(V_2-V_1\right)+\frac{i}{2}p_1\left(V_2-V_1\right)\ (1.10).\]Теперь рассмотрим изохорный процесс ВС. Для него количество теплоты, переданное газу равно:
\[\triangle Q_{BC}=\triangle U_{BC\ }\left(1.11\right).\]так как работа в изохорном процессе равна нулю. Найдем изменений внутренней энергии данного процесса, используя уравнение состояния идеального газа для точек диаграммы B и C:
\[p_1V_2=\nu RT_2\left(1.12\right).\] \[p_2V_2=\nu RT_3\left(1.13\right).\]Вычтем (1.6) из (1.7), получим:
\[p_2V_2-\ p_1V_2=\nu RT_3-\nu RT_2\to {(p}_2-\ p_1)V_2=\nu R\triangle T_{BC}\ (1.14).\]Подставим (1.14) в (1.11) найдем $\triangle Q_{BC}$:
\[\triangle Q_{BC}=\frac{i}{2}{(p}_2-\ p_1)V_2(1.15).\]Получим выражение для $Q^+:$
\[Q^+=\triangle Q_{AB}+\triangle Q_{BC}=\frac{i}{2}{(p}_2-\ p_1)V_2+p_1\left(V_2-V_1\right)+\frac{i}{2}p_1\left(V_2-V_1\right)=\ {\frac{i}{2}p}_2V_2-\ {\frac{i}{2}p}_1V_2+p_1V_2-p_1V_1+\frac{i}{2}p_1V_2-\frac{i}{2}p_1V_1={\frac{i}{2}p}_2V_2+p_1V_2-p_1V_1-\frac{i}{2}p_1V_1={\frac{i}{2}(p}_2V_2-p_1V_1)+p_1{(V}_2-V_1)(1.16).\]Найдем работу, которую совершает газ в круговом процессе. Она равна из геометрического смысла интегралов площади прямоугольника ABCD, соответственно запишем:
\[A_{ABCD}={(p}_2-\ p_1)\left(V_2-V_1\right)\ (1.17).\]Отсюда
\[\eta =\frac{{(p}_2-\ p_1)\left(V_2-V_1\right)}{{\frac{i}{2}(p}_2V_2-p_1V_1)+p_1{(V}_2-V_1)}\ \left(1.18\right).\]Ответ: КПД цикла заданного процесса выражается формулой: $\eta =\frac{{(p}_2-\ p_1)\left(V_2-V_1\right)}{{\frac{i}{2}(p}_2V_2-p_1V_1)+p_1{(V}_2-V_1)}$.
Задание: На рис. 2 изображены изотермы AB и CD. Сравните количества теплоты, получаемые газом, в процессах I и II.
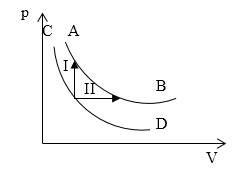
Рис. 2
Решение:
Если AB и СВ -- изотермы, изменения внутренней энергии газа процессах I и II одинаковы: \[\triangle U_I=\triangle U_{II}\left(2.1\right).\]Работа в процессе I равна нулю, так как процесс изохорный, следовательно количество теплоты получаемое газом в процессе I:
\[\triangle Q_I=\triangle U_I\ \left(2.2\right).\]В процессе II работа газом совершается и она больше 0 ($A_I>0).\ $
\[\triangle Q_{II}=\triangle U_{II}+A=\triangle U_I+A\ \to \triangle Q_{II}>\triangle Q_I\left(2.3\right).\]Ответ: Количества теплоты получаемое газом в процессе II больше, чем количество теплоты, получаемое газом в процессе I.












