Что такое циклический процесс
Циклическим называют процесс, начало и конец которого совпадают. На термодинамической диаграмме циклический процесс изображают в виде замкнутой кривой. Сделками указывают направление процесса.
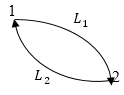
Рис. 1
Различные части кривой иногда для удобства обозначают каким-либо образом. На рис. 1 можно сказать, что система перешла из состояния 1 в состояние 2 по пути $L_1$, а из состояния 2 в состояние 1 по пути $L_2$. Работа в циклическом процессе (рис.1) равна:
\[A=\int\limits^{(2)}_{ \begin{array}{c} \left(1\right) \\ L_1 \end{array} }{pdV}+\int\limits^{(1)}_{ \begin{array}{c} \left(2\right) \\ L_2 \end{array} }{pdV\ \left(1\right).}\]По модулю работа цикла равна площади, которая заключена внутри замкнутой линии, которая изображает цикл. Запишем первое начало термодинамики для имеющегося цикла:
\[\delta Q=dU+pdV\left(2\right),\]где $\delta Q$- элементарное количество теплоты, подведенное к системе, $dU$- элементарное изменение внутренней энергии системы, $pdV$- элементарная работа, совершенная системой.
Проинтегрируем (2) по имеющемуся у нас контуру цикла:
\[\oint{\delta Q}=\oint{dU}+\oint{p}dV\left(2\right).\]Мы знаем, что внутренняя энергия системы -- функция состояния, она не зависит от пути, а зависит только от конечного и начального состояний системы, следовательно:
\[\oint{dU}=0\ \left(3\right).\]В таком случае равенство (2) имеет вид:
\[\oint{\delta Q}=\oint{p}dV=A\left(4\right).\]Выражение (4) означает, что работа (A), совершенная за цикл, произведена за счет количества теплоты, подведенного к системе. Теплота в части 1-2 поступает в систему, в части 2-1 уходит из системы. При обходе цикла по часовой стрелке количество тепла, поступающего в систему, больше, чем выходящее из нее. Следовательно, система совершает положительную работу. При движении от 1 к 2 (рис.1) система сама совершает работу ($A_{12}$), при движении от 2 к 1 над системой совершают работу($A_{21}$). Причем $A_{12}=-A_{21}$.
В каждой точке цикла температура системы определяется уравнением состояния. Определение точек (отрезков диаграмм), где система отдает тепло, а где получает, сводится к решению уравнения $dU+pdV=0.$ Это непростая задача.
Напомню, что эффективность процесса превращения тепла в работу определяется КПД ($\eta $):
\[\eta =\frac{Q_n-{Q'}_{ch}}{Q_n}\left(5\right)\]Цикл Карно
Наиболее простым, но в тоже время очень важным является цикл Карно. Он состоит из двух изотерм и двух адиабат (рис.2).
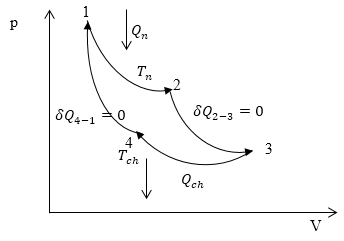
Рис. 2
При выполнении цикла Карно необходимы два термостата. Термостат с температурой $T_n$ называется нагревателем, с температурой $T_{ch}$- холодильник (${T_n>\ T}_{ch}$). При прохождении участков -- адиабат система изолирована от внешней среды в отношении тепла.
Получим формулу расчета КПД для цикла Карно. Рассчитаем количество теплоты, которое получает газ ($Q_n$). Поступление теплоты происходит на изотермическом участке 1-2.
\[Q_n=\int\limits^{\left(2\right)}_{\left(1\right)}{\delta Q}=\int\limits^{\left(2\right)}_{\left(1\right)}{dU}+\int\limits^{\left(2\right)}_{\left(1\right)}{pdV}=RT_nln\frac{V_2}{V_1}\left(6\right),\]Первый интеграл равен нулю, так как мы имеем дело с изотермическим процессом, а второй -- работе при $T_n=const$ (которая рассчитывалась в разделе изотермический процесс). На участке 3-4 система тепло отдает в холодильник при температуре $T_{ch}$. Запишем $Q_{ch}$:
\[Q_{ch}=RT_{ch}ln\frac{V_4}{V_3}\left(7\right).\]Из уравнения адиабаты следует, что
\[T_1V^{\gamma -1}_2=T_2V^{\gamma -1}_3,\ T_1V^{\gamma -1}_1=T_2V^{\gamma -1}_4\to \frac{V_2}{V_1}=\frac{V_3}{V_4}\to {ln \left(\frac{V_2}{V_1}\right)\ }={ln \left(\frac{V_3}{V_4}\right)\ }\left(8\right).\]Подставим (8), (7),(6) в (5), получим КПД цикла Карно:
\[\eta =\frac{RT_nln\frac{V_2}{V_1}-RT_{ch}ln\frac{V_4}{V_3}}{RT_nln\frac{V_2}{V_1}}=\frac{T_n-T_{ch}}{T_n}\left(9\right)\]Формула (9) справедлива для обратимого цикла Карно. Мы получили, что КПД цикла Карно не зависит от конструкции тепловой машины и не зависит от вещества рабочего тела.
Задание: Изобразите цикл Карно параметрах энтропия -- температура.
Решение:
Опишем исходя из рис. 2 участки цикла:
процесс 1-2: Изотермический процесс, происходит с увеличением давления и объема, энтропия растет.
процесс 2-3. Адиабатический или изоэнтропийный. Энтропия постоянна, подвода тепла нет, расширение происходит за счет уменьшения температуры.
процесс 3-4: Изотермический процесс, происходит при уменьшении давления и объема, энтропия уменьшается.
процесс 4-1: Адиабатический или изоэнтропийный. Энтропия постоянна, подвода тепла нет,
за счет совершения работы над газом происходит увеличение его внутренней энергии и, как следствие, температуры. Изобразим перечисленные процессы на графике (рис.3).
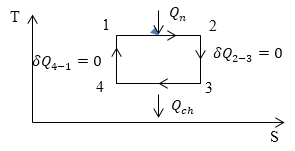
Рис. 3
Задание: Провели два цикла Карно. В первом случае температуру нагревателя увеличили на $\triangle T\ (T_n+\triangle T).$ Во втором температуру холодильника уменьшили на $\triangle T(T_{ch}-\triangle T).\ В\ $каком случае КПД цикла больше?
Решение:
Основанием для решения задачи сделаем выражение для КПД цикла Карно:
\[\eta =1-\frac{T_{ch}}{T_n}\ \left(2.1\right).\]Запишем выражение для двух случаев, указанных в условиях, когда температуру нагревателя увеличивают $\ T_n+\triangle T$, получим:
\[{\eta }_1=1-\frac{T_{ch}}{T_n+\triangle T}\ \left(2.2\right).\]И когда температуру холодильника уменьшают:
\[{\eta }_2=1-\frac{T_{ch}-\triangle T}{T_n}\ \left(2.3\right).\]Найдем разность ${\eta }_1-{\eta }_2$, если ${\eta }_1-{\eta }_2 \[{\eta }_1-{\eta }_2=1-\frac{T_{ch}}{T_n+?T}-1+\frac{T_{ch}-?T}{T_n}=\frac{-T_{ch}\cdot T_n+\left(T_n+?T\right)\cdot \left(T_{ch}-?T\right)}{\left(T_n+?T\right)\left(T_{ch}+?T\right)}=\frac{-T_{ch}\cdot T_n+T_{ch}\cdot T_n-\triangle TT_n+?TT_{ch}-{?T}^2}{\left(T_n+?T\right)\left(T_{ch}+?T\right)}\ \left(2.4\right).\]
В выражении (2.4) знаменатель дроби очевидно больше нуля. Сравним с нулем числитель.
$-\triangle TT_n+\triangle TT_{ch}-{\triangle T}^2-?\ $
Известно, что $T_n>T_{ch}\to \triangle TT_n>\triangle TT_{ch}\to $
\[-\triangle TT_n+\triangle TT_{ch}-{\triangle T}^2Получаем ${\eta }_1Ответ: КПД больше, если уменьшать температуру холодильника.












