Ион молекулы водорода
Физическое описание молекулы принципиально не отличается от физики атома. Но уравнение Шредингера даже для самого простого случая (системы молекулярного типа из трех частиц) невозможно решить аналитически.
Простейшей системой молекулярного типа из трех частиц является ион молекулы водорода ($H^+_2$). Он в своем составе имеет: два протона и один электрон (рис.1). В теории, молекулярный ион водорода исполняет роль, подобную роли атома водорода в атомной физике. Поэтому необходимо иметь для него хотя бы приблизительное решение уравнения Шредингера. Для этого применяют адиабатическое приближение (приближение Борна - Оппенгеймера), в основу которого положено большое различие между массами электронов и ядер. При этом ядра считают неподвижными, а электроны рассматривают как перемещающиеся в стационарном поле, которое создают ядра. Применяя данное приближение, получают решения для конкретных конформаций молекулы (пространственных расположений атомов в молекуле). Для молекул, которые состоят из двух атомов, конформации определены расстояниями между ядрами. Для каждой конформации появляется возможность найти потенциальную энергию молекулы и связать ее с параметрами, которые характеризуют конформацию молекулы. При этом минимум потенциальной энергии соответствует равновесной конформации молекулы.
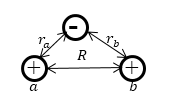
Рисунок 1. Ион молекулы водорода. Автор24 — интернет-биржа студенческих работ
В адиабатическом приближении уравнение Шредингера для иона молекулы водорода можно записать как:
где $r_a$, $r_b$ -- соответствуют обозначениям рис.1. Для того чтобы разделить переменные в уравнении (1) переходят к эллиптическим координатам ($\xi ,\eta ,\varphi $), которые связывают с $r_a$, $r_b$ при помощи формул:
Задача для иона водорода имеет аксиальную симметрию и ее решение от азимутального угла вокруг оси молекулы ($\varphi )$ не зависит.
Решение уравнения Шредингера важно для того, чтобы иметь возможность сравнить результаты опытов и убедиться в возможности применения квантовой механики к молекулярным системам. Кроме того это решение дает возможность проверить справедливость адиабатического приближения, которое используют в теории молекул.
При больших расстояниях $R$ около ядра $a$ при выполнении условия:
уравнение (1) переходит в уравнение для атома водорода с ядром в точке $a$. Аналогично можно рассуждать относительно точки $b$. Волновая функция, которая является решением уравнения Шредингера и существенно отлична от нуля только около точек $a\ и\ b$. Между данными точками $\Psi$ - функция практически равна нулю. При этом перекрытия плотностей электронного облака между протонами нет, ковалентной связи не появляется.
При сближении протонов распределение электронной плотности около них изменяется мало, а между протонами электронная плотность значительно отличается от нуля, причем это связано с симметрией волновой функции. Если волновая функция симметрична, то распределение электронной плотности между протонами не имеет узлов и растет, что приводит к появлению ковалентной связи.
Суммарная энергия системы состоит из отрицательной энергии связи электрона ($E_e$) и положительной энергии взаимодействия протонов ($E_p$). Если $R$ велико, то $E_e\approx -13,6\ эВ$, $E_p\approx 0.$ При $R\to 0$ протоны сливаются друг с другом, и система становится ионом гелия (${He}^+$).
Молекула водорода
Молекула водорода состоит из двух протонов и двух электронов. Это одна из простейших молекул. Обозначим протоны буквами: $a\ и\ b$, а электроны цифрами 1и 2. В том случае, если расстояния между протонами небольшие, то волновые функции сильно перекрываются. Это значит, что каждый электрон принадлежит обоим атомам (между атомами существует обмен электронами). Так появляются обменные силы, которые создают ковалентную связь.
Теоретическая задача в данном случае состоит в нахождении энергии взаимодействия как функции расстояния между протонами. Эта задача часто решается при помощи теории возмущений. В качестве невозмущенного состояния используют основное состояние двух невзаимодействующих атомов водорода.
Для объяснения принципов создания связи между атомами в молекуле водорода положены законы квантовой механики. В первую очередь учитывается волновой характер электрона, который говорит о существовании вероятности обнаружения электрона в непосредственной близости от ядра. В самом простом случае (s- состояние электрона) распределение вероятности имеет сферическую симметрию: так называемое электронное облако является сферой определенного радиуса. Помимо этого учитывается принципиальная неразличимость электронов. Следовательно, если электроны обменяются местами, то в состоянии молекулы водорода ничего не изменится. Такой обмен может состояться только, если ядра атомов в молекуле находятся на малом расстоянии и электронные облака атомов перекрываются. Слияние районов, где могут быть локализованы оба электрона в молекуле водорода, и обозначает появление между ними квантовмеханического обменного взаимодействия. Так, каждый из электронов в молекуле $H_2$ принадлежит то одному, то другому ядру.
Два атома водорода притягиваются и создают молекулу, в том случае, если спины электронов в атомах антипараллельны. В таком случае энергия взаимодействия имеет минимум, если расстояние между протонами составляет порядка Боровского радиуса. Если спины атомов $H$ параллельны, то между атомами на любых расстояниях действуют силы отталкивания, и молекула образоваться не может. Полный спин молекулы водорода равен нулю. Замкнутые оболочки атомов отталкиваются всегда.
Опыты показали, что молекула водорода диамагнитна, так как при отсутствии у молекулы орбитального магнитного момента и при наличии взаимно компенсированных спинах суммарный магнитный момент молекулы равен нулю.
Задание: Связанное состояние из двух протонов может образовываться при имеющемся одном электроне. Подобным состоянием является ион молекулы водорода ($H^+_2$). В таком случае невозможно говорить об обменном взаимодействии. Поясните на классической модели, как реализуется такая связь.
Решение:
В ионе молекулы водорода связь осуществляется единственным электроном, который принадлежит обоим ядрам в равной мере. Как возникают силы притяжения между ядрами, рассмотрим на классическом примере (рис.2).
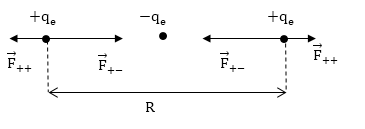
Рисунок 2. Молекулярный ион водорода. Молекула водорода. Автор24 — интернет-биржа студенческих работ
На рис 2. электрон, несущий отрицательный заряд находится посередине между положительными протонами. Ядра (протоны) отталкиваются друг от друга с силой:
\[F_{++}=\frac{q^2_e}{4\pi {\varepsilon }_0R^2}\left(1.1\right).\]При этом ядро и электрон притягиваются друг к другу с силой:
\[F_{+-}=\frac{q^2_e}{4\pi {\varepsilon }_0{\left({R}/{2}\right)}^2}=\frac{4q^2_e}{4\pi {\varepsilon }_0R^2}\left(1.2\right).\]Из формул (1.1) и (1.2) очевидно, что $F_{+-} >F_{++}$. Данный пример показывает только причину возникновения сил притяжения, но классическая физика не может объяснить является ли такое связанное состояние устойчивым.
Задание: Объясните, почему только в синглетном состоянии атомов возможно образование молекулы, в триплетном состоянии молекула образовываться не может.
Решение:
Почему атомы в синглетном и триплетном состояниях ведут себя по разному можно понять исходя из симметрии волновых функций. В синглетном состоянии спиновая волновая функция антисимметрична, в нулевом приближении получается симметричная пространственная функция с разделяющимися переменными:
\[\Psi_s=C_s\left[\Psi_a\left(1\right)\Psi_b\left(2\right)+\Psi_a\left(2\right)\Psi_b\left(1\right)\right]\left(2.1\right),\]где $C_s$ -- постоянная нормировки, $\Psi_a$ -- волновая функция электрона, если он принадлежит ядру $a$, $\Psi_b$ - волновая функция электрона, если он принадлежит ядру $b$. (Функции $\Psi_a$ и $\Psi_b$ считают разными, но они аналитически представлены одинаковыми выражениями).
В триплетном состоянии спиновая волновая функция симметрична, в нулевом приближении получается антисимметричная пространственная функция с разделяющимися переменными:
\[\Psi_a=C_a\left[\Psi_a\left(1\right)\Psi_b\left(2\right)-\Psi_a\left(2\right)\Psi_b\left(1\right)\right]\left(2.1\right),\]где $C_a$ -- постоянная нормировки.
В триплетном состоянии антисимметричная пространственная волновая функция имеет узел в плоскости симметрии, которая проходит посередине между ядрами перпендикулярно прямой, которая их соединяет. Это происходит из-за тождественности электронов:
\[\Psi_a\left(1\right)=\Psi_a\left(2\right),\ \Psi_b\left(1\right)=\Psi_b\left(2\right)\left(2.3\right).\]Эта же причина служит тому, что в синглетном состоянии пространственная волновая функция в той же плоскости симметрии обращается в максимум. Следовательно, в синглетном состоянии плотность вероятности локализации электрона около данной плоскости велика. В триплетном состоянии этаже плотность вероятности стремится к нулю.
В результате в синглетном состоянии начиная с некоторого расстояния кулоновское отталкивание ядер, компенсируется действием электронов противоположного направления (отталкивание изменяется на притяжение). Отрицательный заряд электронов, который появляется между ядрами, стягивает их, при этом возникает связанное состояние. В триплетном состоянии посередине между ядрами компенсирующего действия электронов мало, поскольку мала вероятность нахождения электронов в этой области.
На малых расстояниях (меньше Боровского радиуса) ядра всегда отталкиваются не зависимо от состояния. При этом отталкиваются и протоны (между собой) и электроны (между собой).











