Допустим, что в некоторой среде течет ток, выделим в этой среде гипотетическую замкнутую поверхность S (рис.1).
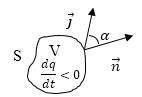
Рис. 1
Исходя из закона сохранения заряда, как эмпирического факта, определим, что заряд, выходящий из объема V, который ограничен поверхностью S в единицу времени ($\frac{\partial q}{\partial t}$), будет равен:
Знак минус учитывает, что если положительный заряд внутри объема уменьшается, то плотность тока направлена из объема V. Напомним, что у замкнутых объёмов положительной нормалью считается внешняя нормаль. Получается, что вектор $d\overrightarrow{S}$ направлен по внешней нормали.
Представим элементарный заряд в виде:
Из выражения (1) получим:
Под знаком интеграла в правой части стоит частная производная, так как плотность заряда может зависеть не только от времени, но и координат. В левой части (3) перейдем от поверхностного интеграла к объемному, получим:
В таком случае выражение (3) можно представить как:
Уравнение (5) должно выполняться для любого объема, следовательно:
Выражение (6) носит название - уравнение непрерывности (уравнение неразрывности). Оно входит в систему уравнений Максвелла в неявном виде. Уравнение непрерывности выражает закон сохранения заряда. Согласно уравнению (6) в точках, которые являются источниками вектора плотности тока ($\overrightarrow{j}$), происходит убывание заряда.
Уравнение неразрывности для стационарных токов
В том случае, если токи не зависят от времени, то уравнение (1) переходит в следующее выражение:
А уравнение (6) в равенство:
Уравнение (8) показывает, что если ток является постоянным, то $\overrightarrow{j}$ не имеет источников. Это значит, что лини тока нигде не начинаются и нигде не заканчиваются. Можно сделать вывод о том, что линии постоянного тока всегда замкнуты. Под линиями токов в данном случае следует понимать лини вектора $\overrightarrow{j}.$ (касательные к которым совпадают с направлением вектора плотности тока в точке касания). Что напрямую следует из (7).
Благодаря замкнутости постоянных токов их можно разложить на совокупность бесконечных замкнутых тонких нитей тока.
Задание: Из уравнения$\ rot\overrightarrow{H}=\frac{4\pi }{c}\overrightarrow{j}+\frac{1}{c}\frac{\partial \overrightarrow{D}}{\partial t}$, которое принадлежит системе уравнений Максвелла (СГС), получите уравнения непрерывности токов и закон сохранения заряда.
Решение:
Используем уравнение
\[rot\overrightarrow{H}=\frac{4\pi }{c}\overrightarrow{j}+\frac{1}{c}\frac{\partial \overrightarrow{D}}{\partial t}\left(1.1\right),\]где $\overrightarrow{H}$ -- напряженность магнитного поля, $c-\ $скорость света в вакууме,$\ \overrightarrow{D}$ -- вектор электрического смещения.
Проведем для него операцию дивергенции ($div\ или\ \nabla $). Получим:
\[\nabla \left(rot\ \overrightarrow{H}\right)=0\left(1.2\right).\] \[\ \nabla \left(\frac{4\pi }{c}\overrightarrow{j}+\frac{1}{c}\frac{\partial \overrightarrow{D}}{\partial t}\right)=\frac{1}{с}\left(4\pi \nabla \overrightarrow{j}+\frac{\partial }{\partial t}\nabla \overrightarrow{D}\right)(1.3).\]мы знаем, что:
\[\nabla \overrightarrow{D}=4\pi \rho \left(1.4\right).\]Подставим (1.4) в (1.3) получим:
\[\frac{1}{с}\left(4\pi \nabla \overrightarrow{j}+\frac{\partial }{\partial t}4\pi \rho \right)=0\left(1.5\right).\]от сюда следует:
\[\nabla \overrightarrow{j}+\frac{\partial }{\partial t}4\pi \rho =0\left(1.6\right).\]или в интегральной форме:
\[\oint\nolimits_S{jdS}+\frac{\partial }{\partial t}\int\nolimits_V{\rho dV}=0\left(1.7\right).\]Соответственно для замкнутых изолированных областей получим:
\[\oint\nolimits_S{jdS}=0\ (1.8)\] \[\int\nolimits_V{\rho dV}=const\ (1.9)\]Это уравнение непрерывности для тока, содержащее в себе закон сохранения заряда -- один из фундаментальных принципов, который подтверждается экспериментом.
Задание: Объясните, как ведет себя нормальная составляющая вектора плотности тока при переходе через границу двух проводящих сред, для стационарных токов. Что можно сказать относительно нормальной составляющей плотности тока для проводника, который находится в непроводящей среде?
Решение:
На поверхности соприкосновения двух проводников может испытывать разрыв непрерывности. Но, его нормальная составляющая ($j_n$) должна быть одинаковой по обе стороны границы сред. В противном случае количество электричества, которое притекает к одной стороне не равно, количеству электричества, которое вытекает с другой стороны. Значит:
\[j_{1n}=j_{2n}\ \left(2.1\right),\]где $j_{1n}-$нормальная составляющая плотность тока в среде (1), $j_{2n}-$нормальная составляющая плотность тока в среде (2).
В непроводящей среде $\overrightarrow{j}=0$. Следовательно, нормальная составляющая к поверхности проводника плотности тока также должна быть равна нулю:
\[j_n=0\ \left(2.2\right).\]Ответ: $j_{1n}=j_{2n}.j_n=0\ .$











