Работа, совершаемая при прохождении тока
Допустим, что между токами с напряжением U переносится заряд величины dq, в таком случае работа, которая совершается равна:
Если по проводнику течет ток $I$, рассмотрим его участок, между концами которого напряжение $U$. За время $dt$ на участке проводника перемещается заряд величины:
В таком случае для работы можно записать:
Мощность тока. Удельная мощность
Если мы работу определили формулой (3), то мощность, которую развивает ток на том же участке, будет равна:
где $\left({\varphi }_1-{\varphi }_2\right)$- разность потенциалов между точками проводника, $\mathcal E_{12}$- ЭДС источника на данном участке.
Данная мощность может идти на совершение участком цепи работы над внешними телами при перемещении участка в пространстве. Или на химические реакции и нагревание выделенного участка.
Удельная мощность -- мощность в единице объема проводника.
Это отношение:
\[P_{ud}=\frac{\triangle P}{\triangle V}\left(5\right),\]где $\triangle P$ изменения мощности в объеме проводника $\triangle V$.
На неоднородном участке цепи на носители тока действуют электростатические силы: ${\overrightarrow{F}}_q=q\overrightarrow{E}$ и сторонние силы: ${\overrightarrow{F}}_{st}=q\overrightarrow{E_{st}}$. Эти силы при движении носителя тока развивают мощность, которая равна:
\[P'=q\left(\overrightarrow{E}+\overrightarrow{E_{st}}\right)\left(\overrightarrow{v}+\overrightarrow{u}\right)\left(6\right),\]где $\overrightarrow{v}$ -- скорость теплового движения молекул, $\overrightarrow{u}$ -- скорость упорядоченного движения носителей тока при наличии поля, $(\overrightarrow{v}+\overrightarrow{u})$- скорость носителей тока в поле, $q$ -- заряд носителя тока (электрона).
Проведем усреднение уравнения (6) по носителям тока, которые находятся в объеме $\triangle V$. В пределах выделенного объема будем считать $\overrightarrow{E},\overrightarrow{E_{st}}$ постоянными, получим:
\[\left\langle P'\right\rangle =q\left(\overrightarrow{E}+\overrightarrow{E_{st}}\right)\left\langle \overrightarrow{v}+\overrightarrow{u}\right\rangle =q\left(\overrightarrow{E}+\overrightarrow{E_{st}}\right)\left\langle \overrightarrow{v}\right\rangle +q\left(\overrightarrow{E}+\overrightarrow{E_{st}}\right)\left\langle \overrightarrow{u}\right\rangle =q\left(\overrightarrow{E}+\overrightarrow{E_{st}}\right)\left\langle \overrightarrow{u}\right\rangle \left(7\right),\]где $\left\langle \overrightarrow{v}\right\rangle =0$. При этом изменение мощности $\triangle P\ $ в$\ \triangle V$ объеме можно найти как произведение:
\[\triangle P=\left\langle P'\right\rangle n\triangle V\ \left(8\right),\]где n∆V -- число носителей тока в заданном объеме. Следовательно, получим:
\[\triangle P=q\left(\overrightarrow{E}+\overrightarrow{E_{st}}\right)\left\langle \overrightarrow{u}\right\rangle n∆V=\overrightarrow{j}\left(\overrightarrow{E}+\overrightarrow{E_{st}}\right)\triangle V\ \left(9\right),\]где $\overrightarrow{j}=q\left\langle \overrightarrow{u}\right\rangle n$ -- вектор плотности тока.
Получено, что удельная мощность проводника с током равна:
\[P_{ud}=\overrightarrow{j}\left(\overrightarrow{E}+\overrightarrow{E_{st}}\right)\left(10\right).\]Выражение (10) является дифференциальной формой уравнения (4).
Задание: Цепь состоит из источника тока и внешнего сопротивления (рис.1). В первом случае подключено сопротивление $R_1$, во втором сопротивление $R_2.\ $ Мощность, выделяющаяся во внешней цепи в обоих случаях равна P. Найдите внутренне сопротивление источника тока.
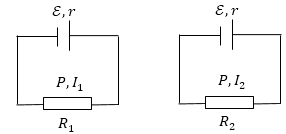
Рис. 1
Решение:
За основу решения задачи примем определение мощности для цепи с током:
\[P=IU=I^2R\ \left(1.1\right),\]где по закону Ома для замкнутой цепи можно записать, что:
\[I=\frac{\mathcal E}{R+r}\left(1.2\right),\]где $\mathcal E$ - ЭДС источника тока, $r$ -- внутреннее сопротивление источника тока.
Согласно условиям задачи мощность тока для цепи с первым сопротивлением и вторым сопротивлением равны, поэтому используем для двух сопротивлений уравнения (1.1) и (1.2), запишем:
\[P={I_1}^2R_1={I_2}^2R_2\to \frac{\mathcal E^2}{{\left(R_1+r\right)}^2}R_1=\frac{\mathcal E^2}{{\left(R_2+r\right)}^2}R_2\left(1.3\right).\]Из (1.3) выразим внутреннее сопротивление r, получим:
\[R_1{\left(R_2+r\right)}^2=R_2{\left(R_1+r\right)}^2\to r=\sqrt{R_1R_2}\left(1.4\right).\]Ответ: $r=\sqrt{R_1R_2}$.
Задание: Три одинаковых сопротивления подключены к источнику постоянного тока (рис.2) внутреннее сопротивление которого равно r. Каким должно быть сопротивление R, для того чтобы мощность, выделяемая на участке AB была максимальной?
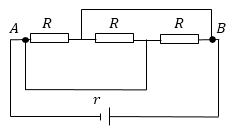
Рис. 2
Решение:
Преобразуем электрическую схему, изображенную на рис.2, получим эквивалентную схему (рис.3):
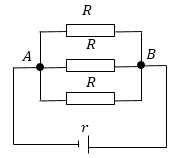
Рис. 3
Результирующее сопротивление ($R_{AB}$) между точками A и B можно найти как:
\[\frac{1}{R_{AB}}=\frac{1}{R}+\frac{1}{R}+\frac{1}{R}\to R_{AB}=\frac{R}{3}\left(2.1\right).\]В таком случае мощность может быть найдена по формуле:
\[P=IU=I^2R_{AB}\ \left(2.2\right),\]где по закону Ома для замкнутой цепи можно записать, что:
\[I=\frac{\mathcal E}{R_{AB}+r}\left(2.3\right),\]где $\mathcal E$ - ЭДС источника тока, $r$ -- внутреннее сопротивление источника тока.
Функция достигает своего экстремума в точке, где ее производная равна нулю. Поэтому найдем производную $\frac{dP}{dR}$ и приравняем ее к нулю:
\[\frac{dP}{dR}={\left[{\left(\frac{\mathcal E}{R_{AB}+r}\right)}^2R_{AB}\right]}'={\left[\mathcal E^2R_{AB}{\left(R_{AB}+r\right)}^{-2}\right]}'=\frac{?^2}{{\left(R_{AB}+r\right)}^2}+\frac{\mathcal E^2R_{AB}\left(-2\right)}{{\left(R_{AB}+r\right)}^3}=\frac{\mathcal E^2\left(R_{AB}+r\right)-2 \mathcal E^2R_{AB}}{{\left(R_{AB}+r\right)}^3}=0\left(2.4\right),\]где ${\left(R_{AB}+r\right)}^3\ne 0$. Следовательно, приравняем числитель к нулю, выразим внешнее сопротивление, получим:
\[\mathcal E^2\left(R_{AB}+r\right)-2 \mathcal E^2R_{AB}=0\to \mathcal E^2r-\mathcal E^2R_{AB}=0\to R_{AB}=r\ \left(2.5\right).\]Используем (2.1), подставим в (2.5), получим:
\[\frac{R}{3}=r\to R=3r.\]Ответ: Мощность максимальна при $R=3r.$












