Закон Ома в виде:
формулу для электросопротивления (R):
где $\rho $ -- удельное сопротивление материала можно использовать для нахождения тока (I) в проводниках в тех случаях, если трубки тока являются цилиндрами с постоянным сечением ($S$). Довольно часто силу тока необходимо вычислить в проводящих средах с другими формами трубок тока. Например, в сферическом конденсаторе, пространство между обкладками в котором заполнено проводящим материалом. В подобном случае формула расчета сопротивления (2) не применима, в связи с тем, что расстояние l различно для разных точек поверхности обкладок, площадь у каждой обкладки разная. Следовательно, закон Ома необходимо представить в другой форме.
Переход от интегральной формы закона Ома к дифференциальной
Найдем связь между вектором плотности тока ($\overrightarrow{j}$) и вектором напряженности электрического поля ($\overrightarrow{E}$) в одной и той же точке проводящей среды. Если вещество изотропно, то $\overrightarrow{j}\uparrow \uparrow \overrightarrow{E}$. Выделим в окрестности рассматриваемой точки гипотетический цилиндр, образующие которого параллельны векторам напряженности поля и плотности тока (рис.1).
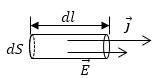
Рис. 1
Через поперечное сечение цилиндра (dS) (рис.1) течет ток, сила которого запишется как:
Напряжение, приложенное к цилиндру можно выразить как:
где $E$ -- напряжённость поля в рассматриваемой точке. Сопротивление цилиндра получит выражение:
Подставим формулы (3),(4),(5) в выражение (1), получим:
Проведем сокращения, получим:
Заменим удельное сопротивление ($\rho $), на удельную проводимость ($\sigma $). Используем то, что векторы напряженности и плотности тока имеют одинаковые направления окончательно запишем:
Уравнение (8) называется законом Ома в дифференциальной форме. В отличие от закона Ома в интегральной форме (1) уравнение (8) содержит величины, которые характеризуют электрическое состояние среды в точке.
Напряженность поля, которая входит в уравнение (8) -- это поле внутри проводящей среды при наличии тока. Однако, если среда однородна, то в большинстве случаев это поле совпадает с электростатическим полем, то есть полем, которое было бы между электродами с таким же напряжением на них что и при наличии тока. Следовательно, в однородном проводнике линии напряженности электростатического поля совпадают с линиями тока.
Дифференциальный закон Ома для анизотропных сред
В анизотропных средах для большинства электрических полей линейная связь между вектором плотности тока и вектором напряженности сохраняется. Однако удельная электрическая проводимость из скаляра переходит в тензор. В таком случае дифференциальный закон Ома выглядит следующим образом:
где индексы $ik$ пробегают значения x,y,z. Таким образом, тензор удельной проводимости имеет девять компонент из них шесть независимых. Тензор удельной проводимости симметричен:
При выборе осей координат, совпадающих с главными осями тензора, не равны нулю только 3 диагональные компоненты: ${\sigma }_{xx}\equiv {\sigma }_1,\ {\sigma }_{yy}\equiv {\sigma }_2,\ {\sigma }_{zz}\equiv {\sigma }_3\ $ - главные значения удельной электрической проводимости.
Задание: Найдите ток утечки через плоский конденсатор, если него подали напряжение U. Пространство между обкладками конденсатора заполнено веществом с удельным сопротивлением $\rho \ $и диэлектрической проницаемостью $\varepsilon $. Емкость конденсатора равна C.
Решение:
За основу решения задачи возьмем закон Ома в дифференциальной форме:
\[j=\frac{1}{\rho }E\ \left(1.1\right).\]Силу тока, если бы мы знали плотность тока можно найти для данного случая, используя формулу:
\[I=\int\limits_S{jdS\ \left(1.2\right).}\]Напряженность поля между обкладками плоского конденсатора может быть найдена в соответствии с формулой:
\[E=\frac{U}{d}\left(1.3\right).\]Подставим закон Ома (1.1) в уравнение (1.2) и используем выражение (1.3):
\[I=\int\limits_S{\frac{1}{\rho }\frac{U}{d}\ dS=\frac{1}{\rho }\frac{U}{d}\ S\ \left(1.4\right).}\]Емкость конденсатора связана с его геометрическими параметрами и веществом, которое заполняет пространство между обкладками:
\[C=\frac{\varepsilon {\varepsilon }_0S}{d}\to \frac{S}{d}=\frac{C}{\varepsilon {\varepsilon }_0}\left(1.5\right).\]Используем полученное отношение $\frac{S}{d}$ подставим в (1.4), получим:
\[I=\frac{1}{\rho }\frac{U}{d}\ \frac{C}{\varepsilon {\varepsilon }_0}.\]Ответ: Ток утечки равен $I=\frac{1}{\rho }\frac{U}{d}\ \frac{C}{\varepsilon {\varepsilon }_0}$.
Задание: Сравните напряженности электрического поля для сечений $S_1$ и $S_2$ (рис.2). Если по проводнику течет постоянный ток ($I=const$).
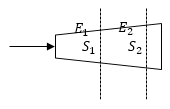
Рис. 2
Решение:
Для решения используем закон Ома в дифференциальной форме:
\[\overrightarrow{j}=\sigma \overrightarrow{E\ }\left(2.1\right).\]Будем считать, что проводник изотропный, запишем (2.1) в скалярном виде:
\[j=\sigma E\ \left(2.2\right).\]При этом плотность силы тока можно записать как:
\[j=\frac{I}{S}\left(2.3\right).\]Подставим (2.3) в (2.2), получим:
\[\frac{I}{S}=уE\left(2.4\right).\]Следовательно,
\[E=\frac{I}{\sigma S}\left(2.5\right).\]Мы получили, что при $I=const,\ \sigma =const$. Напряженность поля зависит только от площади поперечного сечения проводника, причем $E\sim \frac{1}{S}.$
Ответ: Так как $E\sim \frac{1}{S}$, то $E_2\left(S_2\right)












