
Сила взаимодействия параллельных токов. Закон Ампера
Если взять два проводника с электрическими токами, то они будут притягиваться друг к другу, если токи в них направлены одинаково и отталкиваться, если токи текут в противоположных направлениях. Сила взаимодействия, которая приходится на единицу длины проводника, если они параллельны, может быть выражена как:
где $I_1{,I}_2$ -- токи, которые текут в проводниках, $b$- расстояние между проводниками, $в\ системе\ СИ\ {\mu }_0=4\pi \cdot {10}^{-7}\frac{Гн}{м}\ (Генри\ на\ метр)$ магнитная постоянная.
Закон взаимодействия токов был установлен в 1820 г. Ампером. На основании закона Ампера устанавливают единицы силы тока в системах СИ и СГСМ. Так как ампер равен силе постоянного тока, который при течении по двум параллельным бесконечно длинным прямолинейным проводникам бесконечно малого кругового сечения, находящихся на расстоянии 1м друг от друга в вакууме вызывает силу взаимодействия этих проводников равную $2\cdot {10}^{-7}Н$ на каждый метр длины.
Закон Ампера для проводника произвольной формы
Если проводник с током находится в магнитном поле, то на каждый носитель тока действует сила равная:
где $\overrightarrow{v}$ -- скорость теплового движения зарядов, $\overrightarrow{u}$ -- скорость упорядоченного их движения. От заряда, это действие передается проводнику, по которому заряд перемещается. Значит, на проводник с током, который находится в магнитном, поле действует сила.
Выберем элемент проводника с током длины $dl$. Найдем силу ($\overrightarrow{dF}$) с которой действует магнитное поле на выделенный элемент. Усредним выражение (2) по носителям тока, которые находятся в элементе:
где $\overrightarrow{B}$ -- вектор магнитной индукции в точке размещения элемента $dl$. Если n -- концентрация носителей тока в единице объема, S -- площадь поперечного сечения провода в данном месте, тогда N -- число движущихся зарядов в элементе $dl$, равное:
Умножим (3) на количество носителей тока, получим:
Зная, что:
где $\overrightarrow{j}$- вектор плотности тока, а $Sdl=dV$, можно записать:
Из (7) следует, что сила, действующая на единицу объема проводника равна, плотность силы ($f$):
Формулу (7) можно записать в виде:
где $\overrightarrow{j}Sd\overrightarrow{l}=Id\overrightarrow{l}.$
Формула (9) закон Ампера для проводника произвольной формы. Модуль силы Ампера из (9) очевидно равен:
где $\alpha $ -- угол между векторами $\overrightarrow{dl}$ и $\overrightarrow{B}$. Сила Ампера направлена перпендикулярно плоскости, в которой лежат векторы $\overrightarrow{dl}$ и $\overrightarrow{B}$. Силу, которая действует на провод конечной длины можно найти из (10) путем интегрирования по длине проводника:
Силы, которые действуют на проводники с токами, называют силами Ампера.
Направление силы Ампера определяется правилом левой руки (Левую руку надо расположить так, чтобы линии поля входили в ладонь, четыре пальца были направлены по току, тогда отогнутый на 900 большой палец укажет направление силы Ампера).
Задание: Прямой проводник массой m длиной l подвешен горизонтально на двух легких нитях в однородном магнитном поле, вектор индукции этого поля имеет горизонтальное направление перпендикулярное проводнику (рис.1). Найдите силу тока и его направление, который разорвет одну из нитей подвеса. Индукция поля B. Каждая нить разорвется при нагрузке N.
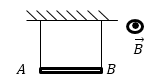
Рис. 1
Решение:
Для решения задачи изобразим силы, которые действуют на проводник (рис.2). Будем считать проводник однородным, тогда можно считать, что точка приложения всех сил - середина проводника. Для того, чтобы сила Ампера была направлена вниз, ток должен течь в направлении из точки А в точку В (рис.2) (На рис.1 магнитное поле изображено, направленным на нас, перпендикулярно плоскости рисунка).
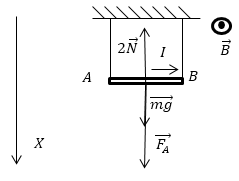
Рис. 2
В таком случае уравнение равновесия сил, приложенных к проводнику с током запишем как:
\[\overrightarrow{mg}+\overrightarrow{F_A}+2\overrightarrow{N}=0\ \left(1.1\right),\]где $\overrightarrow{mg}$ -- сила тяжести, $\overrightarrow{F_A}$ -- сила Ампера, $\overrightarrow{N}$ -- реакция нити (их две).
Спроектируем (1.1) на ось X, получим:
\[mg+F_A-2N=0\ \left(1.2\right).\]Модуль силы Ампера для прямого конечного проводника с током равен:
\[F_A=IBlsin\alpha =IBl\ \left(1.3\right),\]где $\alpha =0$ -- угол между векторами магнитной индукции и направлением течения тока.
Подставим (1.3) в (1.2) выразим силу тока, получим:
\[mg+IBl-2N=0\to I=\frac{2N-mg}{Bl}.\]Ответ: $I=\frac{2N-mg}{Bl}.$ Из точки А и точку В.
Задание: По проводнику в виде половины кольца радиуса R течет постоянный ток силы I. Проводник находится в однородном магнитном поле, индукция которого равна B, поле перпендикулярно плоскости, в которой лежит проводник. Найдите силу Ампера. Провода, которые подводят ток вне поля.
Решение:
Пусть проводник находится в плоскости рисунка (рис.3), тогда линии поля перпендикулярны плоскости рисунка (от нас). Выделим на полукольце бесконечно малый элемент тока dl.
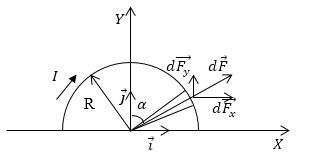
Рис. 3
На элемент тока действует сила Ампера равная:
\[d\overrightarrow{F}=I\left[\overrightarrow{dl}\overrightarrow{B}\right]\ \left(2.1\right).\]Направление силы определяется по правилу левой руки. Выберем координатные оси (рис.3). Тогда элемент силы можно записать через его проекции (${dF}_x,{dF}_y$) как:
\[d\overrightarrow{F}=\overrightarrow{i}{dF}_x+\overrightarrow{j}{dF}_y\left(2.2\right),\]где $\overrightarrow{i}$ и $\overrightarrow{j}$ -- единичные орты. Тогда силу, которая действует на проводник, найдем как интеграл по длине провода L:
\[\overrightarrow{F}=\int\limits_L{d\overrightarrow{F}=}\overrightarrow{i}\int\limits_L{dF_x}+\overrightarrow{j}\int\limits_L{{dF}_y}\left(2.3\right).\]Из-за симметрии интеграл $\int\limits_L{dF_x}=0.$ Тогда
\[\overrightarrow{F}=\overrightarrow{j}\int\limits_L{{dF}_y}\left(2.4\right).\]Рассмотрев рис.3 запишем, что:
\[{dF}_y=dFcos\alpha \left(2.5\right),\]где по закону Ампера для элемента тока запишем, что
\[dF=IBdlsin\left(\overrightarrow{dl}\overrightarrow{B}\right)=IBdl\left(2.6\right).\]По условию $\overrightarrow{dl}\bot \overrightarrow{B}$. Выразим длину дуги dl через радиус R угол $\alpha $, получим:
\[dF=IBRd\alpha \left(2.7\right).\]Тогда
\[{dF}_y=IBRd\alpha cos\alpha \ \left(2.8\right).\]Проведем интегрирование (2.4) при $-\frac{\pi }{2}\le \alpha \le \frac{\pi }{2}\ $подставив (2.8), получим:
\[\overrightarrow{F}=\overrightarrow{j}\int\limits^{\frac{\pi }{2}}_{-\frac{\pi }{2}}{IBRcos\alpha d\alpha }=\overrightarrow{j}IBR\int\limits^{\frac{\pi }{2}}_{-\frac{\pi }{2}}{cos\alpha d\alpha }=2IBR\overrightarrow{j}.\]Ответ: $\overrightarrow{F}=2IBR\overrightarrow{j}.$











