
Экспериментальное установление силы взаимодействия тока и магнитного поля
Магнитное поле не зависимо от источников, которыми оно порождается, токами, постоянными магнитами, проявляет себя, прежде всего, в механическом воздействии на движущиеся заряды. К движущимся зарядам относится и электрические токи.
Рассмотрим силу, которая действует на проводник с током. Ее действие легко обнаружить, если провести простой опыт. Повесить проводник, по которому может течь ток между полюсами постоянного магнита. При включении тока проводник отклонится под действием силы, которая имеет магнитную природу (рис.1).
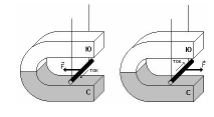
Рис. 1
Ампер первым установил, что проводники, по которым течет электрический ток, взаимодействуют механически (притягиваются или отталкиваются). Он отметил, что природа силы, которая действует на проводник с током в магнитном поле, не является электростатической, а носит особенный характер. Позднее такая сила стала называться силой Ампера. На основе использования силы Ампера действует ряд электроизмерительных приборов магнитоэлектрической системы.
Математические выражения для силы Ампера
Итак, Ампер экспериментально установил, что сила, которая действует в магнитном поле на линейный элемент тока, имеет вид:
Формула (1) называется законом Ампера. Он определяет силу, действующую на элемент тока $\overrightarrow{dl}$ в магнитном поле. Модуль силы $dF$ находится как:
Направлена сила Ампера перпендикулярно плоскости, в которой лежат векторы $\overrightarrow{dl\ }и\ \overrightarrow{B}$. Конкретное направление силы Ампера можно найти с помощью правила левой руки. Левую руку надо расположить так, чтобы линии поля входили в ладонь, четыре пальца были направлены по току, тогда отогнутый на 90 градусов большой палец укажет направление силы Ампера.
Сила Ампера, действующая на провод с током конечной длины может быть найдена как:
где интегрирование проводится по всей длине проводника.
Сила взаимодействия двух прямых параллельных проводников бесконечной длины равна:
где $I_1,I_2$ -- токи, текущие в проводниках, $d$ -- расстояние между проводниками, $l$ -- длины проводников ($l\gg d$), ${\mu }_0=4\pi \cdot {10}^{-7}\frac{Гн}{м}\ (Генри\ на\ метр)$ магнитная постоянная.
Опытное подтверждение связи между электрическими и магнитными полями
Магнитные поля действуют на токи, токи в свою очередь действуют на магнитные поля. Примером может быть опыт Эрстеда. Эрстед помещал магнитную стрелку под прямолинейным проводником с током, параллельно проводу. Стрелка могла вращаться вокруг своей вертикальной оси. Если по проводнику шел ток, то стрелка устанавливалась перпендикулярно проводу. Направление тока изменяли, стрелка разворачивалась на 1800. Такой же эффект происходил, когда провод перемещали под стрелку. На этом опыте впервые была установлена связь между электрическими и магнитными явлениями.
Задание: По двум параллельным, прямолинейным проводникам, имеющим длину l=1м каждый, текут одинаковые токи. Сила взаимодействия этих токов равна $F={10}^{-3}H$. Найдите силу тока, которая течет по проводникам, если расстояние между ними равно d=1см.
Решение:
Прямые параллельные проводники, по которым текут постоянные токи, взаимодействуют друг с другом с силой Ампера, модуль которой запишется в виде:
\[F=\frac{{\mu }_0}{2\pi }\frac{I_1I_2}{d}l=\frac{{\mu }_0}{2\pi }\frac{I^2}{d}l\left(1.1\right),\]где токи $I_1=I_2=I.$ Выразим из (1.1) искомую силу тока, получим:
\[I=\sqrt{\frac{2F\pi d}{l{\mu }_0}}.\]$d=1см={10}^{-2}м$. ${\mu }_0$=$4\pi \cdot {10}^{-7}\frac{Гн}{м}.$ Подставим численные значения величин, проведем вычисления.
\[I=\sqrt{\frac{2\cdot {10}^{-3}\pi \cdot {10}^{-2}}{1\cdot 4\pi \cdot {10}^{-7}}}\approx 7\ \left(А\right).\]Ответ: $I=$7А.
Задание: Прямой провод находится в однородном магнитном поле индукция которого, равна 0,01 Тл. Каков будет угол между направлением вектора индукции и направлением тока, если сила, с которой поле действует на проводник, равна ${10}^{-2}$Н. Длина проводника 0,1 м; сила тока 20 А.
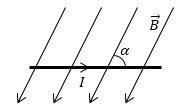
Рис. 2
$\overrightarrow{F}$ направлена перпендикулярно рисунку, от нас.
Решение:
Так как поле по условиям задачи однородное, ток постоянный, за основу решения задачи примем закон Ампера в виде:
\[\overrightarrow{F}=\int{I\left[\overrightarrow{dl}\overrightarrow{B}\right]=I\left[\overrightarrow{l}\overrightarrow{B}\right]\left(2.1\right).}\]Тогда модуль силы Ампера будет равен:
\[F=IBl\cdot sin\alpha \ \left(2.2\right),\]где $\alpha $ -- искомый угол между направлением вектора индукции и направлением тока. Выразим $sin\alpha ,\ $получим:
\[sin\alpha =\frac{F}{IBl}.\]Проведем расчет, все единицы в СИ:
\[sin\alpha =\frac{{10}^{-2}}{20\cdot {10}^{-2}\cdot 0,1}=0,5.\] \[sin\alpha =0,5\to \alpha =\frac{\pi }{6}.\]Ответ: Угол между направлением вектора индукции и направлением тока равен $\frac{\pi }{6}=30{}^\circ .$











