Пространственная когерентность
Допустим, что если пространственные точки $1$ и $2$ не совпадают (рис.1), времена, за которое свет доходит до точки $А$ равны, то говорят о пространственной когерентности волн.
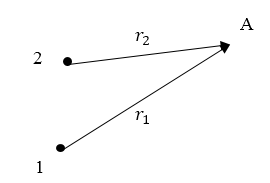
Рисунок 1.
Пусть точка (1) неподвижна, будем поворачивать точку (2). В таком случае, степень когерентности (${\gamma }_{12}$) будет изменяться. Геометрическое место точек, где степень когерентности равно нулю будет некоторая поверхность, которая окружает точку (1). При этом объем, который ограничивает выделенная поверхность, называют объемом когерентности вокруг точки $А$.
В том случае, если источник света характеризуется как монохроматический, имеющий конечные размеры, то говорят о пространственной когерентности. Пространственная когерентность характеризуется шириной, радиусом и углом когерентности.
Этот тип когерентности связан с вариативностью направлений $\overrightarrow{k}$. Направления вектора $\overrightarrow{k}$ характеризуют с помощью единичного вектора $\overrightarrow{e_k}$.
Расстояние ${\rho }_{kog}$ называют длинной пространственной когерентности (радиусом когерентности), его можно определить как:
где $\varphi $ - угловой размер источника световых волн.
Пространственная когерентность волны света около нагретого тела излучения всего несколько длин волн. С увеличением расстояния от источника света степень пространственной когерентности увеличивается.
Формула, с помощью которой устанавливаются угловые размеры протяженного источника, при которых интерференция возможна, имеет вид:
не являются когерентными.
Интерферометр Юнга
В интерферометре Юнга используется метод деления волнового фронта для получения когерентных волн. Юнг был первым, кто создал прибор (установку) для демонстрации явления интерференции. Он пускал яркий пучок солнечного света на экран с маленьким отверстием (щелью). Так получался свет от источника аналогичного точечному монохроматическому источнику ($S$). Световая волна дифрагировала на первой щели, после этого падала на следующий экран с двумя небольшими отверстиями ($S_1\ и\ S_2$). Данные отверстия работают как вторичные монохроматические, точечные источники. Световые пучки вторичных источников перекрываются за экраном $Э$ (рис.2). Наблюдается картина интерференции в области перекрытия получившихся пучков света.
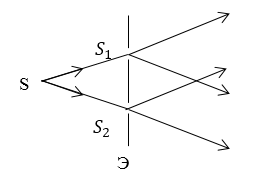
Рисунок 2.
При этом максимумы интенсивности в таком случае будут при:
минимумы при:
Так, интерференционная картина состоит из интерференционных полос, которые лежат на одинаковых расстояниях и направлены под прямым углом к линии $S_1S_2$. Необходимо отметить, что расстояние между щелями $S_{1\ }и\ S_2$ должно быть велико в сравнении с шириной щелей.
Звездный интерферометр Майкельсона
Майкельсон развил идею Физо об измерении угловых размеров астрономических объектов. Он реализовал ее в 1920 г, создав соответствующий интерферометр (рис.3). Роль щелей в данном интерферометре играют подвижные зеркала $З_1\ и\ З_2$. С помощью этих зеркал можно изменять расстояние между щелями (d). После вторичного отражения от зеркал световые лучи направляют через линзу ($Л$) в регистратор интенсивности интерферирующих лучей. Интенсивность в центре определяют по формуле:
где $u_0$ - длина светящегося источника, $\varphi $ - угол, под которым виден источник света.
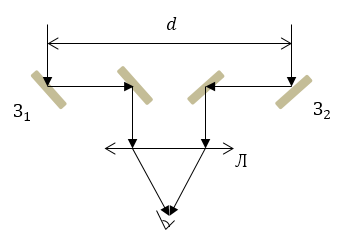
Рисунок 3.
Видимость (видность) интерференционной картины задана функцией:
При увеличении расстояния $d$ от нуля яркость центрального пятна уменьшается, при $d_0$ оно размывается ($V\left(d_0\right)=0$). При этом $d_0$ равно:
По величине $d_0$ находят размер (угловой) звезды:
$\lambda $ - длина волны света.
Изобразите на графике $(V(d))$ видимость интерференционной картины в звездном интерферометре.
Решение:
За основу решения примем выражение для видимости интерференционной картины в звездном интерферометре:
\[V\left(d\right)=\left|\frac{{sin \left(\frac{kd\varphi }{2}\right)\ }}{\frac{kd\varphi }{2}}\right|\left(1.1\right).\]Построим соответствующий выражению (1.1) график:
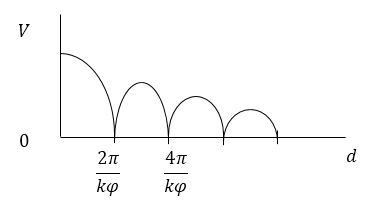
Рисунок 4.
Интерферометры можно использовать для того, чтобы находить размеры некоторых тел. Так, если в интерферометре Юнга на пути одного из интерферирующих лучей разместить перпендикулярно к лучу тонкую стеклянную пластинку (показатель преломления стекла равен $n=1,5$), то центральный максимум сместится в положение, которое занимала изначально пятая светлая полоса. Если длина волны, падающего света равна $\lambda =0,5 мкм$, то какова толщина пластинки?
Решение:
Используем условие максимумов интенсивности интерферирующих лучей:
\[\triangle =m\lambda \left(2.1\right),\]где $\triangle $ - оптическая разность хода волн. Иначе оптическую разность хода лучей можно выразить как:
\[\triangle =nd-d=d\left(n-1\right)\left(2.2\right),\]где $n$ - показатель преломления пластинки, $d$ - ее толщина. Приравняем правые части выражений (2.1) и (2.2), выразим искомую толщину, получим:
\[m\lambda =d\left(n-1\right)\to d=\frac{m\lambda }{n-1}.\]Проведем вычисления:
\[d=\frac{5\cdot 0,5\cdot {10}^{-6}}{1,5-1}=5\cdot {10}^{-6}(м).\]Ответ: $d=5\ мкм.$











