Приближение Френеля
Обычно дифракцию наблюдают в плоскости, которая параллельна преграде (экрану) с отверстиями. Назовем плоскость, в которой проводим наблюдение плоскостью дифракционной картины. Другая плоскость будет плоскостью источников. В обеих плоскостях введем прямоугольные системы координат, причем оси $X$ и $Y$ будут параллельны, а оси $Z$ совпадут (рис.1). Единичный вектор нормали ($\overrightarrow{n}$) направлен в ту сторону, из которой пришло излучение.
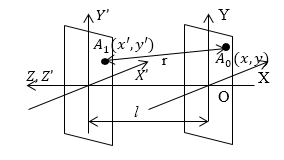
Рисунок 1.
Волну, которая движется к точке $A_0$, будем описывать функцией $\frac{e^{ikr_{01}}}{r_{01}}$. Координатами точки${\ A}_0$ при этом будут в плоскости картины дифракции $(x,y)$. Координатами точки $A_1$ в плоскости источников являются $\left(x',y'\right).$ Тогда элементом площади на поверхности источников станет:
Амплитуда источников пусть задана функцией $\Psi \left(x',y'\right)=A\frac{e^{ikr_{12}}}{r_{12}}.$ В таком случае можно записать:
где $r=\sqrt{l^2+{\left(x-x'\right)}^2+{(y-y')}^2}\ (2')$, здесь $l$ - расстояние между плоскостями. В подынтегральном выражении выражение в квадратных скобках является медленно изменяющейся функцией, если сравнивать ее с множителем $e^{ikr}.$ Значит, данное выражение не оказывает существенного влияния на картину интерференции, только минимально влияет на среднюю величину яркости. Помимо этого углы в функциях косинусов меняются в пределах нуля. Следовательно, данные косинусы можно положить равными единице. В таком случае выражение (2) примет вид:
Упростить формулу (3) можно, если учитывать, что углы $\widehat{\overrightarrow{n}\overrightarrow{r_{12}}}\ и\ \widehat{\overrightarrow{n}\overrightarrow{r_{01}}}$ малы, что можно сформулировать как неравенства:
Используя условие (4) выражение ($2'$) можно разложить в ряд, ограничиваясь членами второго порядка имеем:
Используя выражение (5), преобразуем (3) к виду:
где $r\approx l$. Эту переменную можно вынести из под знака интеграла, так как она медленно изменяется и не влияет на видимость картины интерференции.
Выражение вида (5) называют приближением Френеля, оно приводит к (6). Приближение Френеля используется в большом количестве случаев на практике. Дифракция, которая рассматривается в данном приближении, носит название дифракции Френеля.
Приближение Фраунгофера
Представим выражение как:
подставим его в (6), имеем:
Распределение интенсивности определено в картине дифракции квадратом модуля $Ф(x,y)$. Значит, можно считать, что экспоненты перед знаком интеграла не оказывают влияния на распределение интенсивности в картине дифракции, так как их модуль равен единице. Интегрирование в формуле (7) проводится по всей площади $S'\ (-\infty
Допустим, что отверстие мало, расстояние до плоскости дифракционной картины большое ($l\to \infty $), в таком случае можно считать, что:
Дифракция, которая рассматривается при условии (8) называется фраунгоферовой. Критерием, определяющим возможность принять экспоненту в (8) равной единице служит условие (приближение Фраунгофера):
Так как множитель $\frac{k}{2\pi i}\frac{e^{ikl}}{l}exp(\frac{ik\left(x^2+y^2\right)}{2l})$ в выражении (7), не влияет на распределение интенсивности в картине дифракции, и, учитывая выше сказанное, соответствующую формулу записывают как:
В таком написании выражение (11) служит для нахождения относительных величин интенсивностей в картине дифракции.
Задание: На прямоугольное отверстие со сторонами $a\ и\ b$ падает плоская волна (рис.2), распространяющаяся по оси $Z$. На отверстии фаза и амплитуда волны ($A_0$) постоянны. Как определена амплитуда волны в точке с координатами ($x,y$), если она падает перпендикулярно плоскости щели. Считайте, что можно использовать приближение Фраунгофера.
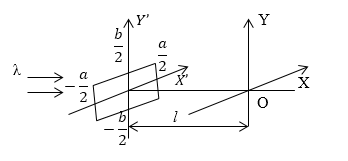
Рисунок 2.
Решение:
Пусть начало координат лежит в центре прямоугольного отверстия. В качестве основы для решения задачи используем приближение Фраунгофера и соответствующую ему формулу:
\[Ф\left(x,y\right)=\int\limits_{S'}{\Psi \left(x',y'\right)exp\left\{-\frac{ik\left(xx'+yy'\right)}{l}\right\}}dx'dy'\left(1.1\right).\]Имея в виду, что функция $\Psi$ имеет размерность амплитуды отнесенной к площади, положим:
\[\Psi \left(x',y'\right)=\frac{А_0}{ab}\left(1.2\right),\]где $A_0$ -- комплексная амплитуда волны. Тогда используя формулу (1.1), (1.2) и полагая $Ф\left(x,y\right)=А\left(x,y\right)$ -- амплитуда волны, имеем:
\[A\left(x,y\right)=\frac{A_0}{ab}\int\limits^{\frac{a}{2}}_{-\frac{a}{2}}{exp\left\{-\frac{ik\left(xx'\right)}{l}dx'\right\}}\int\limits^{\frac{b}{2}}_{-\frac{b}{2}}{exp\left\{-\frac{ik\left(yy'\right)}{l}dy'\right\}}=A_0\frac{sin\alpha }{\alpha }\frac{sin\beta }{\beta }\left(1.3\right),\]где $\alpha =\frac{kax}{2l},\ \beta =\frac{kby}{2l}.$
Ответ: $A\left(x,y\right)=A_0\frac{sin\alpha }{\alpha }\frac{sin\beta }{\beta }$.
Задание: Используя условия и результаты Примера 1, определите интенсивность колебаний в точке с координатами ($x,y$).
Решение:
Используем связь между амплитудой волны и интенсивностью:
\[I\sim {\left|A\right|}^2\left(2.1\right).\]Следовательно, зная, что:
\[A\left(x,y\right)=A_0\frac{sin\alpha }{\alpha }\frac{sin\beta }{\beta }(2.2)\]можно записать:
\[I\left(x,y\right)={\left|A_0\right|}^2\frac{sin^2\alpha }{{\alpha }^2}\frac{sin^2\beta }{{\beta }^2}.\]Ответ: $I\left(x,y\right)={\left|A_0\right|}^2\frac{sin^2\alpha }{{\alpha }^2}\frac{sin^2\beta }{{\beta }^2}.$











