Полосы равной толщины
Допустим, что у нас имеется тонкая пластинка (пленка) в виде клина с углом при вершине равным $\alpha \ $(рис.1). На эту пластинку падает монохроматическая волна. Она отражается от верхней и нижней поверхностей пленки. Данные отраженные волны будут когерентны, что означает, что при их наложении они способны к интерференции.
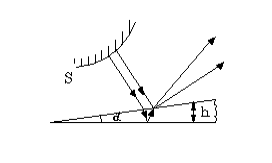
Рисунок 1.
Лучи, которые отражаются от верхней и нижней поверхностей пластинки параллельными не будут. Между лучами образуется разность хода ($\triangle $). В разных точках клина мы получим различную разность хода. Ее можно определить как:
где $h$ - толщина пленки, $n$ -- показатель преломления среды, где распространяется свет.
Пусть лучи падают на клин под углом $90^0$ к поверхности. Кроме того, надо иметь в виду, что когда волна света отражается от среды с большим показателем преломления волна теряет половину длины. Так как показатель преломления у клина больше, чем у воздуха, то свет теряет половину длины при отражении от верхней поверхности клина. В таком случае, для оптической разности хода запишем выражение:
При этом координату $x$ можно связать с толщиной пленки соотношением:
Координаты минимумов интерференции можно найти, зная, что:
Тогда, учитывая (4), найдем $x$:
На конце клина мы будем иметь минимум. Между минимумами можно видеть светлые полосы -- максимумы. Причем полосы на такой пленке расположены на равных расстояниях друг от друга:
Полосы такого типа можно наблюдать на самой пленке. Полоса следует за равной толщиной пленки, отсюда и название «полосы равной толщины».
Полосы равного наклона
Тонкая пластинка (пленка) является плоскопараллельной (имеет одинаковую толщину). На эту пленку попадают лучи под разными углами наклона (рис.2). В таком случае разность хода интерферирующих волн зависит от угла падения лучей. Соответственно минимумы и максимумы интерференции следуют за углами, под которыми падают лучи. Для наблюдения картины интерференции следует собрать отраженные параллельные лучи. Следовательно, зрительный прибор надо сфокусировать на бесконечность. Поэтому считают, что полосы равного наклона наблюдаются на бесконечности. На практике интерференцию в плоскопараллельных пластинах наблюдают, располагая на пути отраженных лучей собирающую линзу. Экран при этом располагают в фокальной плоскости линзы.
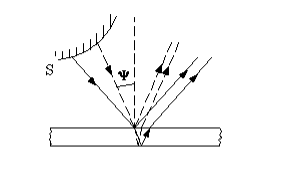
Рисунок 2.
Условие максимума интенсивности для этой пленки имеет вид:
где $\vartheta$ -- угол падения волн на верхнюю поверхность пластинки, $b$ -- толщина пленки.
Задание: Каким должен быть угол наклона клина, если при нормальном падении монохроматического света с длиной волны $\lambda $ расстояние между соседними интерференционными минимумами в отраженном свете равно $\triangle x$?
Решение:
Для ситуации, описанной в задаче, ориентируясь на рис.1 можно записать, что:
\[tg\alpha =\frac{h}{\triangle x}\left(1.1\right),\]где $tg\alpha \approx \alpha \ $, так как угол клина считаем очень маленьким, $\triangle x$ -- расстояние между соседними минимумами. При этом оптическую разность хода можно определить как:
\[\triangle =2hn\left(1.2\right).\]Иначе оптическую разность хода лучей можно выразить:
\[\triangle =\left[2\left(m+1\right)+1\right]\frac{\lambda }{2}-\left[2m+1\right]\frac{\lambda }{2}=\lambda \ \left(m=0,1,2\dots \right)(1.3).\]Приравняем правые части выражений (1.2) и (1.3):
\[2hn=\lambda \left(1.4\right).\]Из уравнения (1.4) выразим h, получим:
\[h=\frac{\lambda }{2n}\left(1.5\right).\]Подставим выражение для h в формулу (1.1), найдем искомый угол:
\[\alpha \approx \frac{\lambda }{2n\triangle x}.\]Ответ: $\alpha \approx \frac{\lambda }{2n\triangle x}.$
Задание: При какой минимальной толщине плоской пленки с параллельными сторонами, показатель преломления которой равен $n>1$, параллельный пучок белого света, падающий на пленку под углом $\alpha =45{}^\circ ,$ при отражении будет иметь длину волны, равную $\lambda $.
Решение:
Запишем условие максимумов при интерференции:
\[\triangle =m\lambda \ при\ m=0,1,2\dots \left(2.1\right).\]Для того чтобы найти выражение для разности хода складывающихся при интерференции лучей обратимся к рис. 3.
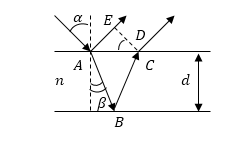
Рисунок 3.
Из рис. 3, учитывая потерю половины волны при отражении света от оптически более плотной среды можно записать:
\[\triangle =\left(AB+BC\right)n-\left(AE-\frac{\lambda }{2}\right)\left(2.2\right).\]При этом очевидно, что $AB=BC$ и из рис. 3 следует, что:
\[AB=\frac{d}{cos\beta }\left(2.3\right).\]Из того же рис. 3 имеем:
\[AD=d\cdot tg\beta ,\ AE=2d\cdot tg\left(\beta \right){sin \left(\alpha \right)\ }\left(2.4\right).\]Подставим полученные выражения в (2.3), (2.4) в формулу (2.2):
\[\triangle =\frac{2n\cdot d}{cos\beta }-2d\cdot tg\left(\beta \right){sin \left(\alpha \right)\ }+\frac{\lambda }{2}\left(2.5\right).\]В соответствии с законом преломления можно записать:
\[\frac{sin (\alpha )}{sin (\beta )}=n\left(2.6\right).\]При этом $tg(\beta )$ можно найти как:
\[tg\left(\beta \right)=\frac{sin\beta }{cos\beta }\left(2.7\right).\]При $m=1$ из условия максимума интерференции (2.1) и выражения (2.5) имеем:
\[\frac{2n\cdot d}{cos\beta }-2d\cdot \frac{sin\beta }{cos\beta }{sin \left(\alpha \right)\ }+\frac{\lambda }{2}=\lambda \to 2\cdot d\cdot n\cdot cos\beta =\frac{\lambda }{2}\left(2.8\right).\]Выразим искомую величину из выражения (2.8), получим:
\[d=\frac{\lambda }{4ncos\beta }\left(2.9\right).\]Учитывая, что:
\[cos\beta =\sqrt{1-sin^2 \beta}=\frac{1}{n}\sqrt{n^2-sin^2\alpha }\left(2.10\right).\]Окончательно для минимальной толщины пленки имеем:
\[d=\frac{\lambda }{4\sqrt{n^2-sin^2\alpha }}.\]Ответ: $d=\frac{\lambda }{4\sqrt{n^2-sin^2\alpha }}.$











