
Распространению света в анизотропной среде свойственна двойственность. Она вызвана тем, что в анизотропных средах любой волновой нормали соответствует луч. Он является характеристикой направления распространения волны света. Луч -- линия, касательная в каждой точке которой, совпадает с направлением вектора плотности потока для энергии волны света в данной точке среды. Для плоской монохроматической волны в однородной изотропной среде лучи перпендикулярны к волновым поверхностям. Следовательно, лучи характеризуют направление переноса энергии с помощью волны, а также направление распространения фронта волны.
Рассмотрим плоскую волну света:
Подставив выражения (1) в уравнения Максвелла, получим формулы:
Волновой вектор $\overrightarrow{k}$ указывает направление распространения фронта волны, то есть, нормален к поверхности одинаковой фазы. Фазовая скорость ($\overrightarrow{v}$) совпадает по направлению с $\overrightarrow{k}$. Направление распространения волны задают вектором $\overrightarrow{n}$, определяемым как:
В общем случае, направление движения волны и направление потока энергии не совпадает. Энергия электромагнитной волны движется с групповой скоростью. Обозначим единичный вектор в направлении луча как:
Тогда можно сказать, что групповая скорость $\overrightarrow{u}$ волны совпадает с направлением $\overrightarrow{\tau }$. Энергия электромагнитной волны движется с групповой скоростью.
Итак, первой особенностью распространения электромагнитной волны в анизотропной среде является то, что, направление групповой и фазовой скорости не совпадают, так как векторы $\overrightarrow{E}$ и $\overrightarrow{D}$ не коллинеарны, направление луча и распространение волны не совпадают.
Фазовая скорость зависит от направления распространения волны и колебаний вектора $\overrightarrow{D}:$
где $n_x=\sqrt{{\varepsilon }_x},n_y=\sqrt{{\varepsilon }_y},n_z=\sqrt{{\varepsilon }_z}-$главные величины показателей преломления анизотропной среды. Надо отметить, что в формуле (5) представлены составляющие фазовой скорости, которые не являются проекцией фазовой скорости волны на оси $X,Y,Z$, а характеризует фазовую скорость волны векторы $\overrightarrow{E}$ и $\overrightarrow{D}$ в которой коллинеарны рассматриваемой оси. Фазовая скорость полностью определена направлением вектора $\overrightarrow{D}$.
Уравнение Френеля для лучевых скоростей
Для того чтобы найти групповую скорость ($\overrightarrow{u}$), отметим, что фронт волны распространяется в направлении $\overrightarrow{n}$, а энергия в направлении $\overrightarrow{\tau }$ (рис.1). Фронт потока энергии расположен перпендикулярно к вектору $\overrightarrow{\tau }$.
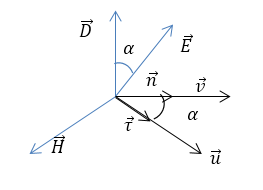
Рисунок 1.
Из рис.1 можно сделать вывод о том, что групповая и фазовая скорости соотносятся как:
где $\alpha $ -- угол между векторами $\overrightarrow{D}$ и $\overrightarrow{E}$ (векторами ${\overrightarrow{u}}$и $\overrightarrow{v}$). Умножим уравнения (2a,b) слева векторно на $\overrightarrow{\tau }$ имеем:
Выразим из (7а) $\overrightarrow{H}$, подставим его в $\left(7b\right)$, получаем:
Учтем выражения (3), (6) и, то что $v=\frac{\omega }{k}$ уравнение (8) запишем в виде:
Если вектор $\overrightarrow{E}$ направлен по одной из главных осей тензора диэлектрической проницаемости (например, оси $X$). В таком случае $\overrightarrow{D}//\overrightarrow{E}$, главные групповые скорости будут совпадать с главными фазовыми скоростями. В таком случае можно считать, что выполняется равенство:
Уравнение Френеля для лучевых скоростей имеет вид:
В том случае, если принять за единичный вектор в направлении $\overrightarrow{E}$, вектор $\overrightarrow{l}$, равный:
уравнение для лучевой скорости можно записать как:
Скорость в направлении луча является групповой.
Две волны, которые распространяются в одном направлении с двумя разными групповыми скоростями, имеют перпендикулярные направления поляризации ($\overrightarrow{E'}\overrightarrow{E''}=0$).
Итак, соотношение между фазовой и лучевой скоростями можно определить, если рассмотреть два положения фронта волны, которые соответствуют близким моментам времени. Вследствие анизотропии среды форма волновой поверхности отлична от сферической. Различие фазовой и лучевой скоростей - проявление анизотропии. Данные скорости различают для монохроматических волн, и в отсутствии дисперсии.
Задание: Даны диагональные элементы тензора диэлектрической проницаемости среды: ${\varepsilon }_x,\ {\varepsilon }_y,\ {\varepsilon }_z.$ Вектор $\overrightarrow{\tau }$ находится в плоскости $XOZ$, и угол между ним и осью $OX$ равен $\alpha .$ Каковы лучевые скорости волн, которые распространяются в избранном направлении?
Решение:
Координаты вектора $\overrightarrow{\tau }$ найдем как:
\[\overrightarrow{\tau }=\left(cos\alpha ,0,sin\alpha \right).\]Для решения задачи используем уравнение волновых нормалей Френеля для лучевых скоростей:
\[\sum\limits^3_{i=1}{\frac{{{\tau }_i}^2v^2_i}{v^2_i-u^2}=0\left(1.1\right).}\]Из условия ${\tau }_y=0$ можно записать:
\[u'=v_y=\frac{c}{\sqrt{{\varepsilon }_y}}\left(1.2\right).\]Для того чтобы найти $u''$ используем (1.1) в виде:
\[\frac{{{\tau }_x}^2v^2_x}{v^2_x-u^2}+\frac{{{\tau }_z}^2v^2_z}{v^2_z-u^2}=0\left(1.4\right).\]Приведем дроби в левой части к одному знаменателю, числитель приравняем к нулю, получим:
\[u^{''}=\sqrt{\frac{v^2_xv^2_z}{{\tau_x}^2v^2_x+{\tau_z}^2v^2_z}}.\]Ответ: $u'=\frac{c}{\sqrt{{\varepsilon }_y}}$, $u^{''}=\sqrt{\frac{v^2_xv^2_z}{{{\tau }_x}^2v^2_x+{{\tau }_z}^2v^2_z}.}$
Задание: Используя данные и решение примера 1, запишите выражения для фазовых скоростей.
Решение:
Из решения Примера 1 следует, что волна поляризована по оси Y. При этом векторы $\overrightarrow{E'}\ и\ \overrightarrow{D'}$ сонаправлены. Фазовая скорость ($v'$) равна:
\[v'=u'=\frac{c}{\sqrt{{\varepsilon }_y}}\left(2.1\right).\]Для второй волны фазовая скорость $v''$ равна:
\[v^{''}=u^{''}cos\alpha (2.2).\]Следовательно:
\[v^{''}=\sqrt{\frac{v^2_xv^2_z}{{{\tau }_x}^2v^2_x+{{\tau }_z}^2v^2_z}}cos\alpha .\]Ответ: $v'=u'=\frac{c}{\sqrt{{\varepsilon }_y}},v^{''}=\sqrt{\frac{v^2_xv^2_z}{{\tau_x}^2v^2_x+{\tau_z}^2v^2_z}}cos\alpha.$











