Изучать процессы, которые протекают в больших системах, весьма сложно из-за огромного числа частиц и их малых размеров. Изучить поведение каждой молекулы весьма затруднительно, из положения выходят, вводя статистические средние величины, когда говорят об описании отдельных частиц. Возникает необходимость установления математической связи (уравнения) между микропараметрами, которые относят к отдельным частицам (масса молекулы, ее скорость и т.д.) и макропараметрами, описывающими систему в целом (температура, давление) Формула, характеризующая состояние системы с учетом микроскопических и макроскопических параметров, называется основным уравнением молекулярно-кинетической теории газов (МКТ).
Связь параметров макромира и микромира
Уравнение состояния идеального газа имеет вид:
где $n=\frac{N}{V}$ -- концентрация частиц в газе, N -- количество частиц, V- объем газа, p -- давление газа, T- термодинамическая температура, $k$- постоянная Больцмана.
Зная выражение для среднеквадратичной скорости:
где $m_0$- масса молекулы. Выразим из (2) kT, получим:
Основное уравнение молекулярно-кинетической теории
Подставим (3) в (1), получим:
Из уравнения мы видим, что давление прямо пропорционально. Налицо связь параметров макромира и микромира.
Уравнение (4) называется основным уравнением молекулярно-кинетической теории. Его можно записать еще и в следующем виде:
где $\rho =m_{0\ }n$ -- плотность газа. При этом смысл уравнений (4) и (5) один и тот же: Отражение взаимовлияния микро и макропараметров системы.
Задание: Найти отношение средних квадратичных скоростей молекул газов с параметрами:
1) $p_1=600\ кПа,\ {\rho }_1=1,2\ \frac{кг}{м^3}$ , 2)$\ p_2=400\ кПа,\ {\rho }_2=0,8\ \frac{кг}{м^3}$.
Решение:
За основу возьмем основное уравнение МКТ в виде:
\[p=\frac{1}{3}\rho {\left\langle v_{kv}\right\rangle }^2\left(1.1\right).\]Выразим из него скорость:
\[\left\langle v_{kv}\right\rangle =\sqrt{\frac{3p}{\rho }}\left(1.2\right).\]Найдем отношение скоростей для газов:
\[\frac{\left\langle v_{kv2}\right\rangle }{\left\langle v_{kv1}\right\rangle }=\sqrt{\frac{3p_2{\rho }_1\ }{{\rho }_23p_1}}=\sqrt{\frac{p_2{\rho }_1\ }{{\rho }_2p_1}}\ \left(1.3\right).\]Проведем расчет (давление можно оставить в тех единицах, которые есть в условиях):
\[\frac{\left\langle v_{kv2}\right\rangle }{\left\langle v_{kv1}\right\rangle }=\sqrt{\frac{400\cdot 1,2}{0,8\cdot 600}}=1\]Ответ: Среднеквадратичные скорости газов с заданными параметрами равны.
Задание: Имеется смесь двух газов. Концентрация первого - $n_1$. второго $n_2$. Средняя кинетическая энергия молекул смеси равна $\left\langle E_k\right\rangle .$ Какова формула для расчета давления смеси этих газов? Система находится в состоянии равновесия.
Решение:
Давление смеси (p) газов равно сумме давлений компонент, поэтому:
\[p=p_1+p_{2\ }\left(2.1\right)\]Запишем основное уравнение МКТ в виде:
\[p=\frac{2}{3}n\left\langle E_k\right\rangle \ \left(2.2\right)\] \[p_1=\frac{2}{3}n_1\left\langle E_k\right\rangle \ (2.3)\] \[p_2=\frac{2}{3}n_2\left\langle E_k\right\rangle (2.4)\] \[p=\frac{2}{3}n\left\langle E_k\right\rangle =\frac{2}{3}n_1\left\langle E_k\right\rangle +\frac{2}{3}n_2\left\langle E_k\right\rangle \to n=n_1+n_2\ (2.5)\]В уравнениях (2.2), (2.3), (2.4) средние кинетические энергии молекул $\left\langle E_k\right\rangle \ $системы в состоянии равновесия во всех частях системы одинаковы.$\ $
Следовательно, искомое давление смеси можно найти, как:
\[p=\frac{2}{3}(n_1+n_2\ )\left\langle E_k\right\rangle (2.6)\]Ответ: Формула для расчета давления смеси двух газов имеет вид: $p=\frac{2}{3}\left(n_1+n_2\ \right)\left\langle E_k\right\rangle .$
Задание: На графике приведен процесс, который проводят с идеальным газом. Сравните скорости молекул газа в точках 1 и 2.
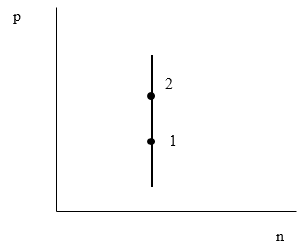
Рис. 1
Решение:
Запишем основное уравнение МКТ в виде:
\[p=n\frac{m_0{\left\langle v_{kv}\right\rangle }^2}{3}\ \left(3.1\right)\]Из графика очевидно, что n - постоянна, следовательно, при большем давлении скорость молекул выше.
Ответ: В состоянии системы отображенном точкой 2 на графике (рис. 1) скорость молекул больше, чем в точке 1.











